题目内容
13.已知等差数列{an},a1=-ll,公差d≠0,且a2,a5,a6成等比数列.(1)求数列{an}的通项公式;
(2)若bn=|an|,求数列{bn}的前n项和Tn.
分析 (1)运用等差数列的通项公式和等比数列的中项的性质,列方程解方程可得公差,进而得到所求通项公式;
(2)由数列{an}的通项公式,可得等差数列中项的正负,运用等差数列的求和公式,分类讨论即可得到所求和.
解答 解:(1)a1=-ll,公差d≠0,且a2,a5,a6成等比数列.
可得a52=a2a6,
即为(-11+4d)2=(-11+d)(-11+5d),
解方程可得d=2,
则数列{an}的通项公式为an=-11+2(n-1)=2n-13;
(2)设等差数列{an}的前n项和为Sn,
则Sn=$\frac{1}{2}$n(a1+an)=$\frac{1}{2}$n(2n-24)=n2-12n,
由an=2n-13,当n≤6时,an<0,当n≥7时,an>0.
bn=|an|,数列{bn}的前n项和Tn.
即有当n≤6时,前n项和Tn=-Sn=12n-n2;
当n≥7时,前n项和Tn=Sn-S6-S6=n2-12n-2×(-36)=n2-12n+72.
综上可得,Tn=$\left\{\begin{array}{l}{12n-{n}^{2},n≤6,n∈N*}\\{{n}^{2}-12n+72,n≥7,n∈N*}\end{array}\right.$.
点评 本题考查等差数列的通项公式和求和公式,和等比数列的中项的性质的运用,考查分类讨论的思想方法,以及化简整理的运算能力,属于中档题.

练习册系列答案
 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
1.已知e是自然对数的底数,函数f(x)=(ax2+x)ex,若f(x)在[-1,1]上是单调增函数,则a的取值范围是( )
| A. | [-$\frac{2}{3}$,0] | B. | (-∞,0)∪[$\frac{2}{3}$,+∞) | C. | [0,$\frac{2}{3}$] | D. | (-∞,-$\frac{2}{3}$]∪[0,+∞) |
8.在复平面内复数z=$\frac{3+4i}{1-i}$(i为虚数单位)对应的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
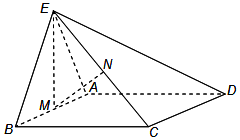 如图,正三角形ABE与菱形ABCD所在的平面互相垂直,AB=2,∠ABC=60°,M是AB的中点,N是CE的中点.
如图,正三角形ABE与菱形ABCD所在的平面互相垂直,AB=2,∠ABC=60°,M是AB的中点,N是CE的中点.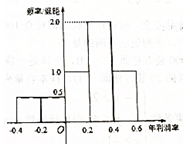 某公司计划明年用不超过6千万元的资金投资于本地养鱼场和远洋捕捞队.经过本地养鱼场年利润率的调研,得到如图所示年利润率的频率分布直方图.对远洋捕捞队的调研结果是:年利润率为60%的可能性为0.6,不赔不赚的可能性为0.2,亏损30%的可能性为0.2.假设该公司投资本地养鱼场的资金为x(x≥0)千万元,投资远洋捕捞队的资金为y(y≥0)千万元.
某公司计划明年用不超过6千万元的资金投资于本地养鱼场和远洋捕捞队.经过本地养鱼场年利润率的调研,得到如图所示年利润率的频率分布直方图.对远洋捕捞队的调研结果是:年利润率为60%的可能性为0.6,不赔不赚的可能性为0.2,亏损30%的可能性为0.2.假设该公司投资本地养鱼场的资金为x(x≥0)千万元,投资远洋捕捞队的资金为y(y≥0)千万元.