题目内容
9.“(x-1)(x+2)=0”是“x=1”的( )| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
分析 根据充分条件和必要条件的定义进行判断即可.
解答 解:由(x-1)(x+2)=0得x=1或x=-2,
则“(x-1)(x+2)=0”是“x=1”的必要不充分条件,
故选:B
点评 本题主要考查充分条件和必要条件的判断,根据充分条件和必要条件的定义是解决本题的关键.

练习册系列答案
相关题目
19.已知函数$f(x)=\left\{\begin{array}{l}({4a-3})x+2a-4,x≤t\\ 2{x^3}-6x,x>t\end{array}\right.$,无论t取何值,函数f(x)在R上总是不单调,则实数a的取值范围是( )
| A. | (-∞,1) | B. | $[{\frac{1}{4},+∞})$ | C. | $[{\frac{3}{4},+∞})$ | D. | $({-∞,\frac{3}{4}}]$ |
17.已知$\frac{π}{4}<x<\frac{π}{2}$,设a=sinx,b=cosx,c=tanx,则( )
| A. | a<b<c | B. | b<a<c | C. | a<c<b | D. | b<c<a |
1.已知e是自然对数的底数,函数f(x)=(ax2+x)ex,若f(x)在[-1,1]上是单调增函数,则a的取值范围是( )
| A. | [-$\frac{2}{3}$,0] | B. | (-∞,0)∪[$\frac{2}{3}$,+∞) | C. | [0,$\frac{2}{3}$] | D. | (-∞,-$\frac{2}{3}$]∪[0,+∞) |
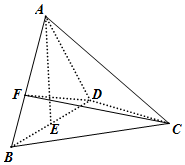 如图,在三棱锥A-BCD中,已知△ABD,△BCD都是边长为2的等边三角形,E为BD中点,且AE⊥平面BCD,F为线段AB上一动点,记$\frac{BF}{BA}=λ$.
如图,在三棱锥A-BCD中,已知△ABD,△BCD都是边长为2的等边三角形,E为BD中点,且AE⊥平面BCD,F为线段AB上一动点,记$\frac{BF}{BA}=λ$.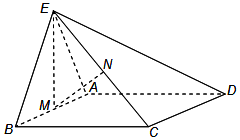 如图,正三角形ABE与菱形ABCD所在的平面互相垂直,AB=2,∠ABC=60°,M是AB的中点,N是CE的中点.
如图,正三角形ABE与菱形ABCD所在的平面互相垂直,AB=2,∠ABC=60°,M是AB的中点,N是CE的中点.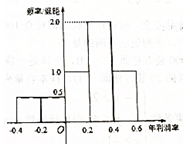 某公司计划明年用不超过6千万元的资金投资于本地养鱼场和远洋捕捞队.经过本地养鱼场年利润率的调研,得到如图所示年利润率的频率分布直方图.对远洋捕捞队的调研结果是:年利润率为60%的可能性为0.6,不赔不赚的可能性为0.2,亏损30%的可能性为0.2.假设该公司投资本地养鱼场的资金为x(x≥0)千万元,投资远洋捕捞队的资金为y(y≥0)千万元.
某公司计划明年用不超过6千万元的资金投资于本地养鱼场和远洋捕捞队.经过本地养鱼场年利润率的调研,得到如图所示年利润率的频率分布直方图.对远洋捕捞队的调研结果是:年利润率为60%的可能性为0.6,不赔不赚的可能性为0.2,亏损30%的可能性为0.2.假设该公司投资本地养鱼场的资金为x(x≥0)千万元,投资远洋捕捞队的资金为y(y≥0)千万元.