题目内容
7.双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$与抛物线y2=2px(p>0)相交于A,B两点,直线AB恰好经过它们的公共焦点F,则双曲线的离心率为1+$\sqrt{2}$.分析 用a,b,c表示出A,B两点坐标,代入抛物线方程得出a,b,c的关系,从而可得离心率.
解答 解:由F为公共焦点可知c=$\frac{p}{2}$,即p=2c,
∵抛物线与双曲线都关于x轴对称,
∴A,B两点关于x轴对称,
∴直线AB的方程为x=c,
代入双曲线方程得y=±$\frac{{b}^{2}}{a}$,即A(c,$\frac{{b}^{2}}{a}$),B(c,-$\frac{{b}^{2}}{a}$).
∵A,B在抛物线上,
∴$\frac{{b}^{4}}{{a}^{2}}$=4c2,又b2=c2-a2,
∴c2-a2=2ac,即e2-2e-1=0,
解得e=1+$\sqrt{2}$或e=1-$\sqrt{2}$(舍).
故答案为:1+$\sqrt{2}$.
点评 本题考查了双曲线与抛物线的性质,属于中档题.

练习册系列答案
相关题目
17.已知$\frac{π}{4}<x<\frac{π}{2}$,设a=sinx,b=cosx,c=tanx,则( )
| A. | a<b<c | B. | b<a<c | C. | a<c<b | D. | b<c<a |
15. 为了解甲、乙两厂产品的质量,从甲厂生产的产品中随机抽取3件样品,从乙厂生产的产品中随机抽取4件样品,测量产品中某种元素的含量(单位:毫克),如图是测量数据的茎叶图.若它们的中位数相同,平均数也相同,则图中的m,n的比值$\frac{m}{n}$=( )
为了解甲、乙两厂产品的质量,从甲厂生产的产品中随机抽取3件样品,从乙厂生产的产品中随机抽取4件样品,测量产品中某种元素的含量(单位:毫克),如图是测量数据的茎叶图.若它们的中位数相同,平均数也相同,则图中的m,n的比值$\frac{m}{n}$=( )
 为了解甲、乙两厂产品的质量,从甲厂生产的产品中随机抽取3件样品,从乙厂生产的产品中随机抽取4件样品,测量产品中某种元素的含量(单位:毫克),如图是测量数据的茎叶图.若它们的中位数相同,平均数也相同,则图中的m,n的比值$\frac{m}{n}$=( )
为了解甲、乙两厂产品的质量,从甲厂生产的产品中随机抽取3件样品,从乙厂生产的产品中随机抽取4件样品,测量产品中某种元素的含量(单位:毫克),如图是测量数据的茎叶图.若它们的中位数相同,平均数也相同,则图中的m,n的比值$\frac{m}{n}$=( )| A. | 1 | B. | $\frac{1}{3}$ | C. | $\frac{8}{3}$ | D. | $\frac{3}{8}$ |
16.已知某中学高三文科班学生的数学与地理的水平测试成绩抽样统计如表:
若抽取学生n人,成绩分为A(优秀),B(良好),C(及格)三个等次,设x,y分别表示数学成绩与地理成绩,例如:表中地理成绩为A等级的共有14+40+10=64(人),数学成绩为B等级且地理成绩为C等级的有8人.已知x与y均为A等级的概率是0.07.
(Ⅰ)设在该样本中,数学成绩的优秀率是30%,求a,b的值;
(Ⅱ)已知a≥7,b≥6,求数学成绩为A等级的人数比C等级的人数多的概率.
| 人数 x y | A | B | C |
| A | 14 | 40 | 10 |
| B | a | 36 | b |
| C | 28 | 8 | 34 |
(Ⅰ)设在该样本中,数学成绩的优秀率是30%,求a,b的值;
(Ⅱ)已知a≥7,b≥6,求数学成绩为A等级的人数比C等级的人数多的概率.
17.已知i是虚数单位,复数z满足(1-i)z=i,则|z|=( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | 1 | D. | $\sqrt{2}$ |
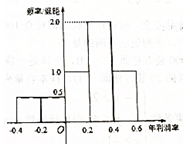 某公司计划明年用不超过6千万元的资金投资于本地养鱼场和远洋捕捞队.经过本地养鱼场年利润率的调研,得到如图所示年利润率的频率分布直方图.对远洋捕捞队的调研结果是:年利润率为60%的可能性为0.6,不赔不赚的可能性为0.2,亏损30%的可能性为0.2.假设该公司投资本地养鱼场的资金为x(x≥0)千万元,投资远洋捕捞队的资金为y(y≥0)千万元.
某公司计划明年用不超过6千万元的资金投资于本地养鱼场和远洋捕捞队.经过本地养鱼场年利润率的调研,得到如图所示年利润率的频率分布直方图.对远洋捕捞队的调研结果是:年利润率为60%的可能性为0.6,不赔不赚的可能性为0.2,亏损30%的可能性为0.2.假设该公司投资本地养鱼场的资金为x(x≥0)千万元,投资远洋捕捞队的资金为y(y≥0)千万元.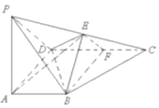 如图,在四棱锥P-ABCD中,PA⊥面ABCD,AB∥CD,CD⊥AD,AD=CD=2AB=2,E,F分别为PC,CD的中点
如图,在四棱锥P-ABCD中,PA⊥面ABCD,AB∥CD,CD⊥AD,AD=CD=2AB=2,E,F分别为PC,CD的中点