题目内容
已知(
+
)n的展开式的第5项的二项式系数与第3项的二项式系数之比为14:3.
(1)求正自然数n的值;
(2)求展开式中的常数项.
| x |
| 2 |
| x2 |
(1)求正自然数n的值;
(2)求展开式中的常数项.
考点:二项式定理的应用
专题:二项式定理
分析:(1)直接利用条件可得意Cn4:Cn2=14:3,化简得n2-5n-50=0,由此求得n=10.
(2)在二项展开式的通项公式中,令x的幂指数等于0,求出r的值,即可求得常数项.
(2)在二项展开式的通项公式中,令x的幂指数等于0,求出r的值,即可求得常数项.
解答:
解:(1)由题意Cn4:Cn2=14:3,化简得n2-5n-50=0,∴n=10,或n=-5(舍去),
∴正自然数n的值为10.
(2)∵展开式的通项公式为 Tr+1=
•2r•x5-
,令5-
=0,求得r=2,
∴常数项为第3项T3=T2+1=22•C102=180.
∴正自然数n的值为10.
(2)∵展开式的通项公式为 Tr+1=
| C | r 10 |
| 5r |
| 2 |
| 5r |
| 2 |
∴常数项为第3项T3=T2+1=22•C102=180.
点评:本题主要考查二项式定理的应用,二项展开式的通项公式,求展开式中某项的系数,二项式系数的性质,属于基础题.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
一个正整数数表如下(表中下一行中的数的个数是上一行中数的个数的2倍):
则第9行中的第4个数是( )
| 第一行 | 1 |
| 第二行 | 2、3 |
| 第三行 | 4、5、6、7 |
| … | … |
| A、132 | B、255 |
| C、259 | D、260 |
已知圆O:x2+y2=25,点A(-3,0)、B(3,0),一条抛物线以圆O的切线为准线且过点A和B,则这列抛物线的焦点的轨迹方程是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知△ABC中,
•
=
•
且|
+
|=|
|,则△ABC的形状为( )
| AB |
| BC |
| AC |
| CB |
| AC |
| AB |
| BC |
| A、锐角三角形 |
| B、钝角三角形 |
| C、等腰直角三角形 |
| D、等边三角形 |
下列三视图表示的几何体是( )
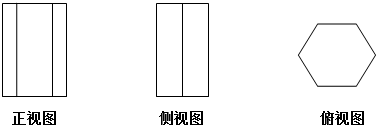

| A、正六棱柱 | B、正六棱锥 |
| C、正六棱台 | D、正六边形 |
圆ρ=
(cosθ+sinθ)的圆心坐标是( )
| 2 |
A、(
| ||||
B、(1,
| ||||
C、(
| ||||
D、(2,
|