题目内容

17．在△ABC中，命题p：“B≠60°“，命题q：“△ABC的三个内角A，B，C不成等差数列“，那么p是q的
（　　）
A．充分不必要条件B．必要不充分条件
C．充分必要条件D．既不充分也不必要条件

分析 由B≠60°，则（A+C）-2B=π-B-2B≠0，?△ABC的三个内角A，B，C不成等差数列．

解答 解：命题p：“B≠60°“则（A+C）-2B=π-B-2B≠0，?命题q：“△ABC的三个内角A，B，C不成等差数列“，
故选：C．

点评 本题考查了三角形内角和定理、等差数列、简易逻辑的判定方法，考查了推理能力与计算能力，属于基础题．

练习册系列答案
相关题目
7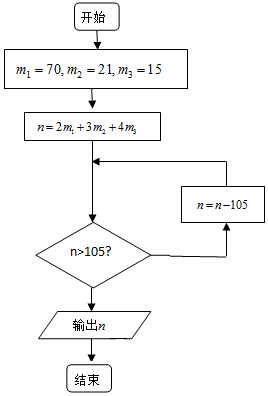．明朝数学家程大位将“孙子定理”（也称“中国剩余定理”）编成易于上口的《孙子口诀》：三人同行七十稀，五树梅花廿一支，七子团圆正半月，除百零五便得知．已知正整数n被3除余2，被5除余3，被7除余4，求n的最小值．按此口诀的算法如图，则输出n的结果为（　　）
A．53B．54C．158D．263
8．定义：如果函数y=f（x）在定义域内给定区间[a，b]上存在x0（a＜x0＜b），满足f（x0）=$\frac{f（b）-f（a）}{b-a}$，则称函数y=f（x）是[a，b]上的“平均值函数”，x0而是它的一个均值点．
例如y=|x|是[-2，2]上的“平均值函数”，0就是它的均值点．给出以下命题：
①函数f（x）=sinx-1是[-π，π]上的“平均值函数”；
②若y=f（x）是[a，b]上的“平均值函数”，则它的均值点x0≤$\frac{a+b}{2}$；
③若函数f（x）=x2+mx-1是[-1，1]上的“平均值函数”，则实数m∈（-2，0）；
④若f（x）=lnx是区间[a，b]（b＞a≥1）上的“平均值函数”，x0是它的一个均值点，则lnx0＜$\frac{1}{{\sqrt{ab}}}$．
其中的真命题有①③④（写出所有真命题的序号）．
5．已知等比数列{an}中，a3=4，a6=$\frac{1}{2}$，则公比q=$\frac{1}{2}$．
12．已知x，y满足约束条件$\left\{\begin{array}{l}{x-y≥0}\\{x+y≥1}\\{x≤2}\end{array}\right.$，则z=$\frac{y+3}{x}$的最小值为（　　）
A．-1B．7C．$\frac{5}{2}$D．1
2．已知直线l：$\left\{{\begin{array}{l}{x=1+tcosα}\\{y=tsinα}\end{array}}$（其中t为参数，α为倾斜角）．以坐标原点O为极点，x轴的正半轴为极轴，建立极坐标系，曲线C的极坐标方程为ρ=$\frac{cosθ}{{{{sin}^2}θ}}$．
（1）求C的直角坐标方程，并求C的焦点F的直角坐标；
（2）已知点P（1，0），若直线l与C相交于A，B两点，且$\frac{1}{{|{PA}|}}+\frac{1}{{|{PB}|}}$=2，求△FAB的面积．
9．若复数z=（sinα-$\frac{1}{3}$）+i（cosα-$\frac{2\sqrt{2}}{3}$）是纯虚数（i是虚数单位），则tanα的值为（　　）
A．$\frac{\sqrt{2}}{4}$B．-$\frac{\sqrt{2}}{4}$C．2$\sqrt{2}$D．-2$\sqrt{2}$
6．函数y=2x+1-2x2的图象大致是（　　）
A．B．C．D．
7．宋元时期数学名著《算学启蒙》中有关于“松竹并生”的问题：松长五尺，竹长两尺，松日自半，竹日自倍，松竹何日而长等．图1是源于其思想的一个程序框图，若输入的a，b分别为4，2，则输出的n等于（　　）
A．2B．3C．4D．5

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网