题目内容
9.若复数z=(sinα-$\frac{1}{3}$)+i(cosα-$\frac{2\sqrt{2}}{3}$)是纯虚数(i是虚数单位),则tanα的值为( )| A. | $\frac{\sqrt{2}}{4}$ | B. | -$\frac{\sqrt{2}}{4}$ | C. | 2$\sqrt{2}$ | D. | -2$\sqrt{2}$ |
分析 复数z=(sinα-$\frac{1}{3}$)+i(cosα-$\frac{2\sqrt{2}}{3}$)是纯虚数(i是虚数单位),可得sinα-$\frac{1}{3}$=0,cosα-$\frac{2\sqrt{2}}{3}$≠0,cosα=-$\frac{2\sqrt{2}}{3}$,即可得出.
解答 解:∵复数z=(sinα-$\frac{1}{3}$)+i(cosα-$\frac{2\sqrt{2}}{3}$)是纯虚数(i是虚数单位),
∴sinα-$\frac{1}{3}$=0,cosα-$\frac{2\sqrt{2}}{3}$≠0,
∴sinα=$\frac{1}{3}$,cosα=-$\frac{2\sqrt{2}}{3}$,
∴tanα=-$\frac{\sqrt{2}}{4}$.
故选:B.
点评 本题考查了复数的运算法则、纯虚数的定义、同角三角函数基本关系式,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
19.$\frac{{{i^{2017}}}}{1-2i}$=( )
| A. | $-\frac{2}{5}+\frac{1}{5}i$ | B. | $\frac{2}{5}-\frac{1}{5}i$ | C. | $\frac{2}{5}+\frac{1}{5}i$ | D. | $-\frac{2}{5}-\frac{1}{5}i$ |
17.在△ABC中,命题p:“B≠60°“,命题q:“△ABC的三个内角A,B,C不成等差数列“,那么p是q的
( )
( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
 一儿童游乐场拟建造一个“蛋筒”型游乐设施,其轴截面如图中实线所示.ABCD是等腰梯形,AB=20米,∠CBF=α(F在AB的延长线上,α为锐角).圆E与AD,BC都相切,且其半径长为100-80sinα米.EO是垂直于AB的一个立柱,则当sinα的值设计为多少时,立柱EO最矮?
一儿童游乐场拟建造一个“蛋筒”型游乐设施,其轴截面如图中实线所示.ABCD是等腰梯形,AB=20米,∠CBF=α(F在AB的延长线上,α为锐角).圆E与AD,BC都相切,且其半径长为100-80sinα米.EO是垂直于AB的一个立柱,则当sinα的值设计为多少时,立柱EO最矮?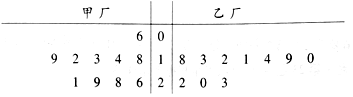 某种产品的产量以其质量指标值(单位:克)衡量,质量指标值越大表明质量越好,且质量指标值大于17时,该产品为优等品,现在为了解甲、乙两厂产品的质量,从两厂生产的产品中分别随机抽取10件样品,测量样品的质量指标值,得到如图所示的茎叶图.
某种产品的产量以其质量指标值(单位:克)衡量,质量指标值越大表明质量越好,且质量指标值大于17时,该产品为优等品,现在为了解甲、乙两厂产品的质量,从两厂生产的产品中分别随机抽取10件样品,测量样品的质量指标值,得到如图所示的茎叶图.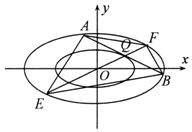 在直角坐标系xOy中,椭圆C1:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的离心率为$\frac{{\sqrt{2}}}{2}$,左、右焦点分别是F1,F2,P为椭圆C1上任意一点,|PF1|2+|PF2|2的最小值为8.
在直角坐标系xOy中,椭圆C1:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的离心率为$\frac{{\sqrt{2}}}{2}$,左、右焦点分别是F1,F2,P为椭圆C1上任意一点,|PF1|2+|PF2|2的最小值为8.