题目内容

6．函数y=2x+1-2x2的图象大致是（　　）
A．B．C．D．

分析 判断当x→-∞时y的变化趋势，并计算当x=3时的函数值，结合选项得出答案．

解答 解：当x→-∞时，2x+1→0，2x2→+∞，∴y→-∞，排除C，D；
又当x=3时，y=24-2×32=16-18=-2＜0，排除B，
故选A，

点评 本题考查了函数图象的判断，属于中档题．

练习册系列答案
相关题目
16．已知曲线C的参数方程为$\left\{{\begin{array}{l}{x=2cosθ}\\{y=\sqrt{3}sinθ}\end{array}（{θ为参数}）}\right.$，在同一平面直角坐标系中，将曲线C上的点按坐标变换$\left\{{\begin{array}{l}{x'=\frac{1}{2}x}\\{y'=\frac{1}{{\sqrt{3}}}y}\end{array}}\right.$得到曲线C'，以原点为极点，x轴的正半轴为极轴，建立极坐标系．
（Ⅰ）求曲线C'的极坐标方程；
（Ⅱ）若过点$A（\frac{3}{2}，π）$（极坐标）且倾斜角为$\frac{π}{6}$的直线l与曲线C'交于M，N两点，弦MN的中点为P，求$\frac{|AP|}{|AM|•|AN|}$的值．
17．在△ABC中，命题p：“B≠60°“，命题q：“△ABC的三个内角A，B，C不成等差数列“，那么p是q的
（　　）
A．充分不必要条件B．必要不充分条件
C．充分必要条件D．既不充分也不必要条件
14．己知椭圆C：$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞1）的左焦点F与抛物线y2=-4x的焦点重合，直线x-y+$\frac{\sqrt{2}}{2}$=0与以原点O为圆心，以椭圆的离心率e为半径的圆相切．
（I ）求该椭圆C的方程
（II）设点P坐标为（-$\frac{1}{8}$，0），若|PA|=|PB|，求直线AB的方程．
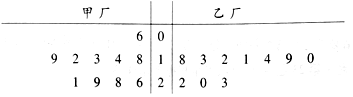1．某种产品的产量以其质量指标值（单位：克）衡量，质量指标值越大表明质量越好，且质量指标值大于17时，该产品为优等品，现在为了解甲、乙两厂产品的质量，从两厂生产的产品中分别随机抽取10件样品，测量样品的质量指标值，得到如图所示的茎叶图．
（1）试用上述样本数据估计甲、乙两厂产品的优等品率．
（2）从甲厂10件样品中抽取2件，乙厂10件中抽取1件，将3件中优等品的件数记为x，求x的分布列和数学期望；
（3）从甲厂的10件样品中有放回地随机抽取3件（每件抽取一件），也从乙厂的10件样品中有放回地随机抽取3件（每次抽取一件），求抽到的优等品甲厂恰比乙厂多2件的概率．
11．已知公差为d的等差数列{an}前n项和为Sn，若有确定正整数n0，对任意正整数m，${S}_{{n}_{0}}$•${S}_{{n}_{0}+m}$＜0恒成立，则下列说法错误的是（　　）
A．a1•d＜0B．|Sn|有最小值
C．${a}_{{n}_{0}}$•${a}_{{n}_{0}+1}$＞0D．${a}_{{n}_{0}+1}•{a}_{{n}_{0}+2}$＞0
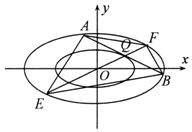18．在直角坐标系xOy中，椭圆C1：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（{a＞b＞0}）$的离心率为$\frac{{\sqrt{2}}}{2}$，左、右焦点分别是F1，F2，P为椭圆C1上任意一点，|PF1|2+|PF2|2的最小值为8．
（I）求椭圆C1的方程；
（II）设椭圆C2：$\frac{{2{x^2}}}{a^2}+\frac{{2{y^2}}}{b^2}=1，Q（{{x_0}，{y_0}}）$为椭圆C2上一点，过点Q的直线交椭圆C1于A，B两点，且Q为线段AB的中点，过O，Q两点的直线交椭圆C1于E，F两点．
（i）求证：直线AB的方程为x0x+2y0y=2；
（ii）当Q在椭圆C2上移动时，四边形AEBF的面积是否为定值？若是，求出该定值；不是，请说明理由．
15．执行如图所示程序框图，若输入的k=4，则输出的s=（　　）
A．$\frac{1}{3}$B．$\frac{4}{5}$C．$\frac{5}{6}$D．$\frac{6}{7}$
16．设Sn为等差数列{an}的前n项和，且a3=5，S6=42，则S9=117．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网