题目内容

在△ABC中，“sinA＞
3
2
”是“A＞
π
3
”的（　　）
A、充分不必要条件
B、必要不充分条件
C、充要条件
D、既不充分也不必要条件
考点：必要条件、充分条件与充要条件的判断
专题：简易逻辑
分析：先看由sinA＞
3
2
能否得到A＞
π
3
：A∈(0，
π
2
]时，根据y=sinx在(0，
π
2
]上的单调性即可得到A＞
π
3
，而A∈(
π
2
，π)时显然满足A＞
π
3
；然后看A＞
π
3
能否得到sinA＞
3
2
，这个可通过y=sinx在（0，π）上的图象判断出得不到sinA＞
3
2
，并可举反例比如A=
5π
6
．综合这两个方面便可得到“sinA＞
3
2
”是“A＞
π
3
”的充分不必要条件．
解答： 解：△ABC中，若A∈（0，
π
2
]，
3
2
=sin
π
3
，所以sinA＞
3
2
得到A＞
π
3
；
若A∈(
π
2
，π)，显然得到A＞
π
3
；
即sinA＞
3
2
能得到A＞
π
3
；
而A＞
π
3
，得不到sinA＞
3
2
，比如，A=
5π
6
＞
π
3
，sin
5π
6
=
1
2
＜
3
2
；
∴“sinA＞
3
2
”是“A＞
π
3
”的充分不必要条件．
故选A．
点评：考查正弦函数y=sinx在（0，π）的图象及单调性，充分条件，必要条件，以及充分不必要条件的概念．
练习册系列答案
相关题目
椭圆的中心是原点O，它的短轴长为2
2
，椭圆与双曲线
x2
3
-y2=1有共同的焦点．
（1）求椭圆的方程；
（2）过点A（3，0）的直线与椭圆相交于不同的P、Q两点，求该直线斜率k的取值范围．
设棋子在正四面体ABCD的表面从一个顶点等可能地移向另外三个顶点中的一个顶点．现抛掷骰子根据其点数决定棋子是否移动：若投出的点数是奇数，则棋子不动；若投出的点数是偶数，棋子移动到另一顶点．若棋子的初始位置在顶点A，则投了2次骰子，棋子才到达顶点B的概率是
5
36
；投了3次骰子，棋子恰巧在顶点B的概率是
 
．
某种产品的广告费支出x与销售额y （单位：百万元）之间有如下的对应数据：
x24568
y3040506070
根据上表提供的数据 算出
.
x
=5，
.
y
=50，
5
i=1
xi2=145，
5
i=1
xiyi=1390用最小二乘法求出y关于x的线性回归方程为
 
．
与向量
a
=（
3
-1，
3
+1）夹角角为
π
4
的单位向量是（　　）
A、（-
1
2
，
3
2
）或（
3
2
，
1
2
）
B、（-
1
2
，-
3
2
）或（
1
2
，-
3
2
）
C、（-
1
2
，-
3
2
）或（-
1
2
，
3
2
）
D、（
1
2
，
3
2
）或（-
3
2
，
1
2
）
已知集合M={x|
1
x
≤1}，N={x|y=lg（1-x）}，则下列关系中正确的是（　　）
A、（∁RM）∩N=∅
B、M∪N=R
C、M?N
D、（∁RM）∪N=R
在△ABC中，已知角A，B，C所对的边分别为a，b，c，且a=3，c=8，B=60°，则△ABC的周长是（　　）
A、18B、19C、16D、17
函数y=sinx在区间[
π
3
，
2π
3
]上的值域是
 
．
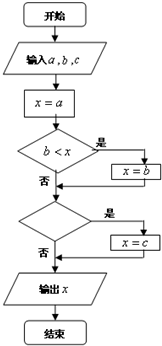如图所示程序框图中，如果输入三个实数a、b、c，要求输出这三个数中最小的数，那么在空白的判断框中，应该填入下面四个选项中的（　　）
A、c＜xB、x＜c
C、c＜bD、b＜c

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网