题目内容
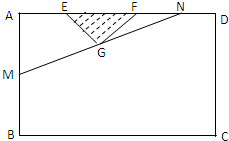 某小区想利用一矩形空地ABCD建造市民健身广场,设计时决定保留空地边上的一个水塘(如图中阴影部分),水塘可近似看作一个等腰直角三角形,其中AD=60m,AB=40m,且△EFG中,∠EGF=90°,经测量得到AE=10m,EF=20m.为保证安全同时考虑美观,健身广场周围准备加设一个保护栏.设计时经过点G作一条直线交AB,DF于M,N,从而得到五边形MBCDN的市民健身广场.
某小区想利用一矩形空地ABCD建造市民健身广场,设计时决定保留空地边上的一个水塘(如图中阴影部分),水塘可近似看作一个等腰直角三角形,其中AD=60m,AB=40m,且△EFG中,∠EGF=90°,经测量得到AE=10m,EF=20m.为保证安全同时考虑美观,健身广场周围准备加设一个保护栏.设计时经过点G作一条直线交AB,DF于M,N,从而得到五边形MBCDN的市民健身广场.(Ⅰ)假设DN=x(m),试将五边形MBCDN的面积y表示为x的函数,并注明函数的定义域;
(Ⅱ)问:应如何设计,可使市民健身广场的面积最大?并求出健身广场的最大面积.
考点:解三角形的实际应用
专题:应用题,不等式的解法及应用
分析:(Ⅰ)作GH⊥EF,垂足为H,过M作MT∥BC交CD于T,则有SMBCDW=SMBCT+SMTDN=(40-AM)×60+
(x+60)×AM,可解得y=2400-
,从而可得五边形MBCDN的面积y表示为x的函数;
(2)将函数变形,利用基本不等式,可求市民健身广场的面积最大值.
| 1 |
| 2 |
| 5(60-x)2 |
| 40-x |
(2)将函数变形,利用基本不等式,可求市民健身广场的面积最大值.
解答:
解:(Ⅰ)作GH⊥EF,垂足为H,
因为DN=x,所以NH=40-x,NA=60-x,
因为
=
,
所以
=
,所以AM=
,
过M作MT∥BC交CD于T,则
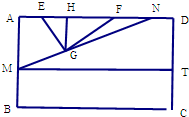
SMBCDW=SMBCT+SMTDN=(40-AM)×60+
(x+60)×AM,
所以y=(40-
)×60+
×
=2400-
,
由于N与F重合时,AM=AF=30适合条件,故x∈(0,30],
(Ⅱ)y=2400-
=2400-5[(40-x)+
+40],
所以当且仅当40-x=
,即x=20∈(0,30]时,y取得最大值2000,
答:当DN=20m时,得到的市民健身广场面积最大,最大面积为2000m2.
因为DN=x,所以NH=40-x,NA=60-x,
因为
| NH |
| HG |
| NA |
| AM |
所以
| 40-x |
| 10 |
| 60-x |
| AM |
| 600-10x |
| 40-x |
过M作MT∥BC交CD于T,则

SMBCDW=SMBCT+SMTDN=(40-AM)×60+
| 1 |
| 2 |
所以y=(40-
| 600-10x |
| 40-x |
| 1 |
| 2 |
| (x+60)(600-10x) |
| 40-x |
| 5(60-x)2 |
| 40-x |
由于N与F重合时,AM=AF=30适合条件,故x∈(0,30],
(Ⅱ)y=2400-
| 5(60-x)2 |
| 40-x |
| 400 |
| 40-x |
所以当且仅当40-x=
| 400 |
| 40-x |
答:当DN=20m时,得到的市民健身广场面积最大,最大面积为2000m2.
点评:本题主要考察了解三角形的实际应用,不等式的解法及应用,属于中档题.基本不等式应注意其使用条件:一正二定三相等.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
某几何体三视图如下图所示,则该几何体的表面积为( )


| A、16-π | B、16+π |
| C、16-2π | D、16+2π |
已知集合M={x|
≤1},N={x|y=lg(1-x)},则下列关系中正确的是( )
| 1 |
| x |
| A、(∁RM)∩N=∅ |
| B、M∪N=R |
| C、M?N |
| D、(∁RM)∪N=R |
已知等比数列{an}的首项为
,公比为-
,其前n项和为Sn,则Sn的最大值为( )
| 3 |
| 2 |
| 1 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
 (理科) 为了近似求出圆周率的值,有人设计如下方法来进行随机模拟:如图,双曲线
(理科) 为了近似求出圆周率的值,有人设计如下方法来进行随机模拟:如图,双曲线