题目内容
抛物线y2=4x上与焦点相距最近的点的坐标是（ ）
| A、（0，0） |
| B、（1，2） |
| C、（1，-2） |
| D、以上都不是 |
考点：抛物线的简单性质
专题：圆锥曲线的定义、性质与方程
分析：根据抛物线的性质，抛物线上的点到原点的距离等于到准线的距离，可得原点满足条件．
解答：
解：抛物线y2=4x的准线方程为x=-1，
根据抛物线点到焦点的距离等于点到准线的距离，
及抛物线y2=4x点的横坐标x≥0，
可得可得所求点的横坐标为0．
故抛物线y2=4x上与焦点相距最近的点的坐标是（0，0），
故选：A
根据抛物线点到焦点的距离等于点到准线的距离，
及抛物线y2=4x点的横坐标x≥0，
可得可得所求点的横坐标为0．
故抛物线y2=4x上与焦点相距最近的点的坐标是（0，0），
故选：A
点评：本题要找出抛物线上到焦点的距离最近点的横坐标，着重考查了抛物线的标准方程与简单性质，属于基础题．
练习册系列答案
活力课时同步练习册系列答案
学业测评一课一测系列答案
相关题目
已知等比数列{an}的首项为
，公比为-
，其前n项和为Sn，则Sn的最大值为（ ）
| 3 |
| 2 |
| 1 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
不等式x2-2x-3＞0的解集是（ ）
| A、（-1，3） |
| B、（3，+∞） |
| C、（-∞，-1）∪（3，+∞） |
| D、（-∞，-1） |
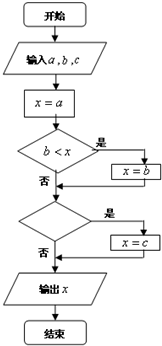如图所示程序框图中，如果输入三个实数a、b、c，要求输出这三个数中最小的数，那么在空白的判断框中，应该填入下面四个选项中的（ ）| A、c＜x | B、x＜c |
| C、c＜b | D、b＜c |