题目内容
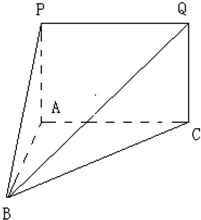
如图，已知PA⊥平面ABC，QC⊥平面ABC，PA=QC，求证：PQ∥平面ABC
考点：直线与平面平行的判定
专题：空间位置关系与距离
分析：由PA⊥平面ABC，QC⊥平面ABC，得PA∥QC，又PA=QC，得四边形PAQC是平行四边形，从而得PQ∥AC，根据线面平行的判定可证．
解答：
证明：∵PA⊥平面ABC，QC⊥平面ABC，
∴PA∥QC，
由PA=QC，
∴四边形PAQC是平行四边形，
∴PQ∥AC，
PQ?平面ABC，AC?平面ABC，
∴PQ∥平面ABC．
∴PA∥QC，
由PA=QC，
∴四边形PAQC是平行四边形，
∴PQ∥AC，
PQ?平面ABC，AC?平面ABC，
∴PQ∥平面ABC．
点评：本题考查线面平行，考查体积的计算，考查学生分析解决问题的能力，正确运用线面平行的判定定理是关键．
练习册系列答案
相关题目
（理科） 为了近似求出圆周率的值，有人设计如下方法来进行随机模拟：如图，双曲线已知
=（2，-1，3），
=（-4，2，x），且
⊥
，则x=（ ）
| a |
| b |
| a |
| b |
| A、10 | ||
B、
| ||
| C、3 | ||
D、-
|
某几何体三视图如下图所示，则该几何体的表面积为（ ）
| A、16-π | B、16+π |
| C、16-2π | D、16+2π |
