题目内容
11.已知函数f(x)=x2+alnx.(Ⅰ)当a=1时,求曲线f(x)在点(1,f(1))处的切线方程;
(Ⅱ)当a=-2时,求函数f(x)的极值;
(Ⅲ)若函数g(x)=f(x)+$\frac{2}{x}$在[1,4]上是减函数,求实数a的取值范围.
分析 (Ⅰ)求出f(1),f′(1),代入切线方程即可;
(Ⅱ)求出f(x)的导数,解关于导函数的不等式,求出函数的单调区间,从而求出函数的极值即可;
(Ⅲ)由g(x)=x2+alnx+$\frac{2}{x}$,得g′(x),由g'(x)≤0在[1,4]上恒成立,可得a≤$\frac{2}{x}$-2x2在[1,4]上恒成立.构造函数φ(x)=$\frac{2}{x}$-2x2,求其最小值即可.
解答 解:(Ⅰ)a=1时,f(x)=x2+lnx,f′(x)=2x+$\frac{1}{x}$,
故f(1)=1,f′(1)=3,
故切线方程是:y-1=3(x-1),
即3x-y-2=0;
(Ⅱ)函数f(x)的定义域为(0,+∞)
当a=-2时,f′(x)=2x-$\frac{2}{x}$=$\frac{2(x+1)(x-1)}{x}$,
令f′(x)>0,解得:x>1,令f′(x)<0,解得:0<x<1,
故函数f(x)单调递减区间是(0,1),单调递增区间是(1,+∞)
∴极小值是f(1)=1,没有极大值;
(Ⅲ)由g(x)=x2+alnx+$\frac{2}{x}$,得g′(x)=2x+$\frac{a}{x}$-$\frac{2}{{x}^{2}}$,
又函数g(x)=x2+alnx+$\frac{2}{x}$为[1,4]上的单调减函数,
则g'(x)≤0在[1,4]上恒成立,
所以不等式2x+$\frac{a}{x}$-$\frac{2}{{x}^{2}}$≤0在[1,4]上恒成立,
即a≤$\frac{2}{x}$-2x2在[1,4]上恒成立,
设φ(x)=$\frac{2}{x}$-2x2,显然ϕ(x)在[1,4]上为减函数,
所以ϕ(x)的最小值为ϕ(4)=-$\frac{63}{2}$,
∴a的取值范围是a≤-$\frac{63}{2}$.
点评 本题考查利用倒数研究函数的单调性,考查闭区间上的恒成立问题,突出转化思想与构造函数的思想的运用,属于难题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | $\frac{4\sqrt{3}}{3}$ | B. | $\frac{16\sqrt{3}}{3}$ | C. | $\frac{32\sqrt{3}}{3}$ | D. | $\frac{64\sqrt{3}}{3}$ |
| A. | f(x)=$\frac{1}{x-1}$,g(x)=$\frac{x+1}{{x}^{2}-1}$ | B. | f(x)=|x+1|,g(x)=$\sqrt{{x}^{2}+2x+1}$ | ||
| C. | f(x)=x0,g(x)=1 | D. | f(x)=3x+2(x≥0),g(x)=2+3x |
| A. | ac>bc | B. | $\frac{b}{a}$>1 | C. | |a|>|b| | D. | ($\frac{1}{2}$)a<($\frac{1}{2}$)b |
| A. | $\sqrt{3}$ | B. | 3 | C. | $\sqrt{6}$ | D. | $\frac{{\sqrt{6}}}{2}$ |
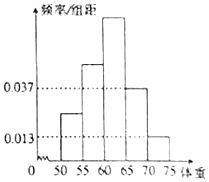 为了解今年某校高三毕业班想参军的学生体重情况,将所得的数据整理后,画出了频率分布直方图(如图).已知图中从左到右的前3个小组的频率之比为1:2:3,其中第2小组的频数为24.
为了解今年某校高三毕业班想参军的学生体重情况,将所得的数据整理后,画出了频率分布直方图(如图).已知图中从左到右的前3个小组的频率之比为1:2:3,其中第2小组的频数为24.