题目内容
14.已知扇形OAB的面积为1,周长为4,则弦AB的长度为( )| A. | 2 | B. | $\frac{2}{sin1}$ | C. | 2sin1 | D. | sin2 |
分析 设圆的半径为rcm,弧长为lcm,则$\left\{\begin{array}{l}{\frac{1}{2}lr=1}\\{l+2r=4}\end{array}\right.$,可得l,r,然后,求解扇形的圆心角,可求弦AB的长.
解答 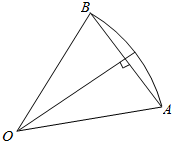 解:设圆的半径为rcm,弧长为lcm,则$\left\{\begin{array}{l}{\frac{1}{2}lr=1}\\{l+2r=4}\end{array}\right.$,
解:设圆的半径为rcm,弧长为lcm,则$\left\{\begin{array}{l}{\frac{1}{2}lr=1}\\{l+2r=4}\end{array}\right.$,
∴l=2,r=1,
∴圆心角为$\frac{l}{r}$=2,
过点O作OH⊥AB于H,则∠AOH=1弧度,
∴AH=1•sin1=sin1(cm),
∴AB=2sin1(cm).
故选:C.
点评 本题重点考查了弧长公式、圆心角公式等知识,属于中档题,解题关键是灵活运用公式进行求解问题.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
19.下列各组函数中,表示同一函数的一组是( )
| A. | f(x)=$\frac{1}{x-1}$,g(x)=$\frac{x+1}{{x}^{2}-1}$ | B. | f(x)=|x+1|,g(x)=$\sqrt{{x}^{2}+2x+1}$ | ||
| C. | f(x)=x0,g(x)=1 | D. | f(x)=3x+2(x≥0),g(x)=2+3x |
3.若a<b<0,则下列不等式成立的是( )
| A. | ac>bc | B. | $\frac{b}{a}$>1 | C. | |a|>|b| | D. | ($\frac{1}{2}$)a<($\frac{1}{2}$)b |