题目内容
已知f（x）=
，若f（lg（log210））=5，那么f（lg（lg2））的值为多少？
| 4x+1 |
| 2x |
考点：对数的运算性质
专题：函数的性质及应用
分析：由于f（x）=
=2x+
，可得f（-x）=2-x+2x=f（x）．即可得出．
| 4x+1 |
| 2x |
| 1 |
| 2x |
解答：
解：∵f（x）=
=2x+
，∴f（-x）=2-x+2x=f（x）．
∵f（lg（log210））=5，lg（log210）+lg（lg2）=lg(
•lg2)=0，
∴f（lg（lg2））=5．
| 4x+1 |
| 2x |
| 1 |
| 2x |
∵f（lg（log210））=5，lg（log210）+lg（lg2）=lg(
| 1 |
| lg2 |
∴f（lg（lg2））=5．
点评：本题考查了对数与指数幂的运算法则，考查了推理能力与计算能力，属于中档题．
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
设函数f（x），g（x）在[a，b]上均可导，且f′（x）＜g′（x），则当a＜x＜b时，有（ ）
| A、f（x）＞g（x） |
| B、f（x）+g（a）＜g（x）+f（a） |
| C、f（x）＜g（x） |
| D、f（x）+g（b）＜g（x）+f（b） |
如图是函数f（x）的导函数f′（x）的图象，则下面判断正确的是（ ）
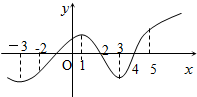
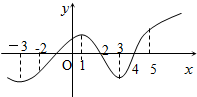
| A、函数f（x）在区间（-2，1）上单调递增 |
| B、函数f（x）在x=1处取得极大值 |
| C、函数f（x）在（4，5）上单调递增 |
| D、当x=4时，f（x）取极大值 |