题目内容
某种产品有一等品、二等品、次品三个等级,其中一等品和二等品都是正品.现有6件该产品,从中随机抽取2件来进行检测.
(1)若6件产品中有一等品3件、二等品2件、次品1件.
①抽检的2件产品全是一等品的概率是多少?
②抽检的2件产品中恰有1件是二等品的概率是多少?
(2)如果抽检的2件产品中至多有1件是次品的概率不小于
,则6件产品中次品最多有多少件?
(1)若6件产品中有一等品3件、二等品2件、次品1件.
①抽检的2件产品全是一等品的概率是多少?
②抽检的2件产品中恰有1件是二等品的概率是多少?
(2)如果抽检的2件产品中至多有1件是次品的概率不小于
| 4 |
| 5 |
考点:相互独立事件的概率乘法公式,互斥事件的概率加法公式
专题:概率与统计
分析:(1)从6件产品中随机抽取2件,有
=15种抽法.①从3件一等品中随机抽取2件,有
种抽法,②抽取的2件产品中恰有1件是二等品的抽法有8种,由此求得①、②的概率.
(2)设6件产品中有x件次品(0≤x<6,x∈N),分类讨论,利用相互独立事件的概率乘法公式,求出“抽检的2件产品中至多有1件是次品的概率”,从而得出结论.
| C | 2 6 |
| C | 2 3 |
(2)设6件产品中有x件次品(0≤x<6,x∈N),分类讨论,利用相互独立事件的概率乘法公式,求出“抽检的2件产品中至多有1件是次品的概率”,从而得出结论.
解答:
解:(1)记“抽取的2件产品全是一等品”为事件A,
“抽取的2件产品中恰有1件是二等品”为事件B.
从6件产品中随机抽取2件,有
=15种抽法.
①从3件一等品中随机抽取2件,有
=3种抽法,故P(A)=
=
;
②抽取的2件产品中恰有1件是二等品的抽法有8种,故P(B)=
.
(2)设6件产品中有x件次品(0≤x<6,x∈N).
当x=0时,抽检的2件产品中至多有1件是次品的概率等于1;
当x=1时,抽检的2件产品中至多有1件是次品的概率等于
=1,
当x=2时,则抽检的2件产品中至多有1件是次品的概率为
=
;
当x=3时,则抽检的2件产品中至多有1件是次品的概率为
=
;
当x=4时,则抽检的2件产品中至多有1件是次品的概率为
=
;
当x=5时,则抽检的2件产品中至多有1件是次品的概率为
=
.
于是,x的最大值等于3.
答:抽检的2件产品全是一等品的概率是
;抽检的2件产品中恰有1件是二等品的概率是
.若抽检的2件产品中至多有1件次品的概率不小于
,则6件产品中次品最多有3件.
“抽取的2件产品中恰有1件是二等品”为事件B.
从6件产品中随机抽取2件,有
| C | 2 6 |
①从3件一等品中随机抽取2件,有
| C | 2 3 |
| 3 |
| 15 |
| 1 |
| 5 |
②抽取的2件产品中恰有1件是二等品的抽法有8种,故P(B)=
| 8 |
| 15 |
(2)设6件产品中有x件次品(0≤x<6,x∈N).
当x=0时,抽检的2件产品中至多有1件是次品的概率等于1;
当x=1时,抽检的2件产品中至多有1件是次品的概率等于
| ||||||
|
当x=2时,则抽检的2件产品中至多有1件是次品的概率为
| ||||||
|
| 14 |
| 15 |
当x=3时,则抽检的2件产品中至多有1件是次品的概率为
| ||||||
|
| 4 |
| 5 |
当x=4时,则抽检的2件产品中至多有1件是次品的概率为
| ||||||
|
| 3 |
| 5 |
当x=5时,则抽检的2件产品中至多有1件是次品的概率为
| ||||
|
| 1 |
| 3 |
于是,x的最大值等于3.
答:抽检的2件产品全是一等品的概率是
| 1 |
| 5 |
| 8 |
| 15 |
| 4 |
| 5 |
点评:本题主要考查相互独立事件的概率乘法公式,体现了分类讨论的数学思想,属于中档题.

练习册系列答案
 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
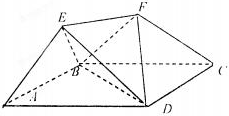 如图,底面ABCD是边长为2的菱形,且∠BAD=
如图,底面ABCD是边长为2的菱形,且∠BAD=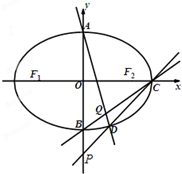 已知F1,F2分别是椭圆E:
已知F1,F2分别是椭圆E: