题目内容
在直角坐标系xOy上取两个定点A1(-2,0),A2(2,0),再取两个动点N1(0,m),N2(0,n),且mn=3.
(1)求直线A1N1与A2N2交点的轨迹M的方程;
(2)已知点G(1,0)和G′(-1,0),点P在轨迹M上运动,现以P为圆心,PG为半径作圆P,试探究是否存在一个以点G′(-1,0)为圆心的定圆,总与圆P内切?若存在,求出该定圆的方程;若不存在,请说明理由.
(1)求直线A1N1与A2N2交点的轨迹M的方程;
(2)已知点G(1,0)和G′(-1,0),点P在轨迹M上运动,现以P为圆心,PG为半径作圆P,试探究是否存在一个以点G′(-1,0)为圆心的定圆,总与圆P内切?若存在,求出该定圆的方程;若不存在,请说明理由.
考点:直线和圆的方程的应用,轨迹方程
专题:综合题,直线与圆,圆锥曲线的定义、性质与方程
分析:( )由直线方程的点斜式列出A1N1和A2N2的方程,联解并结合mn=3化简整理得
+
=1,再由N1、N2不与原点重合,可得直线A1N1与A2N2交点的轨迹M的方程;
(2)由题意,点G(1,0)和G′(-1,0)为椭圆的焦点,则PG+PG′=4,从而PG′=4-PG,即可得出结论.
| x2 |
| 4 |
| y2 |
| 3 |
(2)由题意,点G(1,0)和G′(-1,0)为椭圆的焦点,则PG+PG′=4,从而PG′=4-PG,即可得出结论.
解答:
解:(1)依题意知直线A1N1的方程为:y=
(x+2)…①;
直线A2N2的方程为:y=-
(x-2)…②
设Q(x,y)是直线A1N1与A2N2交点,①、②相乘,得y2=-
(x2-4)
由mn=3整理得:
+
=1
∵N1、N2不与原点重合,可得点A1(-2,0),A2(2,0)不在轨迹M上,
∴轨迹M的方程为:
+
=1(x≠±2).
(2)由题意,点G(1,0)和G′(-1,0)为椭圆的焦点,则PG+PG′=4,
∴PG′=4-PG,
∴点G′(-1,0)为圆心,4为半径的定圆,总与圆P内切,
方程为(x+1)2+y2=16.
| m |
| 2 |
直线A2N2的方程为:y=-
| n |
| 2 |
设Q(x,y)是直线A1N1与A2N2交点,①、②相乘,得y2=-
| mn |
| 4 |
由mn=3整理得:
| x2 |
| 4 |
| y2 |
| 3 |
∵N1、N2不与原点重合,可得点A1(-2,0),A2(2,0)不在轨迹M上,
∴轨迹M的方程为:
| x2 |
| 4 |
| y2 |
| 3 |
(2)由题意,点G(1,0)和G′(-1,0)为椭圆的焦点,则PG+PG′=4,
∴PG′=4-PG,
∴点G′(-1,0)为圆心,4为半径的定圆,总与圆P内切,
方程为(x+1)2+y2=16.
点评:本题着重考查了动点轨迹的求法、椭圆的标准方程与简单几何性质、圆与圆的位置关系等知识,属于中档题.

练习册系列答案
相关题目
已知复数z满足(1-i)z=2,则z的模|z|等于( )
| A、1 | ||
B、
| ||
| C、2 | ||
| D、4 |
240°化成弧度制是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
下列函数中,以为π最小正周期的偶函数,且在(0,
)内递增的是( )
| π |
| 2 |
| A、y=sin|x| |
| B、y=|sinx| |
| C、y=|cosx| |
| D、y=cos|x| |
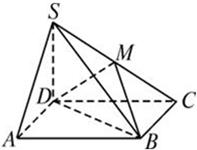 如图,ABCD是平行四边形,S是平面ABCD外一点,M为SC的中点.求证:SA∥平面MDB.
如图,ABCD是平行四边形,S是平面ABCD外一点,M为SC的中点.求证:SA∥平面MDB.