题目内容
设函数fn(x)=x-(n2+2n)x2(其中n∈N*),区间In={x|fn(x)>0}.
(Ⅰ)求区间In的长度(注:区间(α,β)的长度定义为β-α);
(Ⅱ)把区间In的长度记作数列{an},令Sn=a1+a2+…+an,证明:
≤Sn<
.
(Ⅰ)求区间In的长度(注:区间(α,β)的长度定义为β-α);
(Ⅱ)把区间In的长度记作数列{an},令Sn=a1+a2+…+an,证明:
| 1 |
| 3 |
| 3 |
| 4 |
考点:数列的应用
专题:综合题,等差数列与等比数列
分析:(Ⅰ)根据In={x|fn(x)>0},解不等式,即可求区间In的长度(注:区间(α,β)的长度定义为β-α);
(Ⅱ)利用裂项法求和,即可证明结论.
(Ⅱ)利用裂项法求和,即可证明结论.
解答:
(Ⅰ)解:由fn(x)>0,得x-(n2+2n)x2>0,解得0<x<
,…(3分)
即In=(0,
),所以区间In的长度为
-0=
; …(6分)
(Ⅱ)证明:由(Ⅰ)知an=
=
(
-
),…(7分)
则Sn=
[(
-
)+(
-
)+…+(
-
)]=
(1+
-
-
)=
-
(
+
)…(10分)
因为n∈N*,故Sn<
,…(11分)
又易知Sn=
-
(
+
)单增,故Sn≥S1=
-
(
+
)=
,
综上
≤Sn<
.…(12分)
| 1 |
| n2+2n |
即In=(0,
| 1 |
| n2+2n |
| 1 |
| n2+2n |
| 1 |
| n2+2n |
(Ⅱ)证明:由(Ⅰ)知an=
| 1 |
| n2+2n |
| 1 |
| 2 |
| 1 |
| n |
| 1 |
| n+2 |
则Sn=
| 1 |
| 2 |
| 1 |
| 1 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| n |
| 1 |
| n+2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| n+1 |
| 1 |
| n+2 |
| 3 |
| 4 |
| 1 |
| 2 |
| 1 |
| n+1 |
| 1 |
| n+2 |
因为n∈N*,故Sn<
| 3 |
| 4 |
又易知Sn=
| 3 |
| 4 |
| 1 |
| 2 |
| 1 |
| n+1 |
| 1 |
| n+2 |
| 3 |
| 4 |
| 1 |
| 2 |
| 1 |
| 1+1 |
| 1 |
| 1+2 |
| 1 |
| 3 |
综上
| 1 |
| 3 |
| 3 |
| 4 |
点评:本题考查数列的通项与求和,考查裂项法的运用,确定数列的通项是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
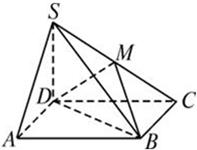 如图,ABCD是平行四边形,S是平面ABCD外一点,M为SC的中点.求证:SA∥平面MDB.
如图,ABCD是平行四边形,S是平面ABCD外一点,M为SC的中点.求证:SA∥平面MDB.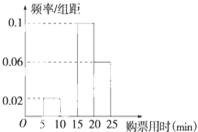 某车站在春运期间为了了解旅客购票情况,随机抽样调查了100名旅客从开始在售票窗口排队到购到车票所用的时间t(以下简称为购票用时,单位为min),如图是这次调查统计分析得到的数据(如图所示).
某车站在春运期间为了了解旅客购票情况,随机抽样调查了100名旅客从开始在售票窗口排队到购到车票所用的时间t(以下简称为购票用时,单位为min),如图是这次调查统计分析得到的数据(如图所示).