题目内容
已知A、B、C分别为△ABC的三边a、b、c所对的角，向量
=（sinA，sinB），
=（cosB，cosA），且
•
=sin2C．
（1）求角C的大小；
（2）若a，c，b成等差数列，且
•（
-
）=18，求边c的长．
| m |
| n |
| m |
| n |
（1）求角C的大小；
（2）若a，c，b成等差数列，且
| CA |
| AB |
| AC |
考点：平面向量的综合题
专题：三角函数的求值,平面向量及应用
分析：先根据数量积的定义把给的条件化成三角函数，再利用三角形内角和定理结合诱导公式、两角和与差公式、二倍角公式进行化简得到关于C的方程求解；
把条件“
•（
-
）=18”用三角形的边角表示出来是第二问的关键，然后利用余弦定理求出c的值．
把条件“
| CA |
| AB |
| AC |
解答：
解 （Ⅰ）由已知得
•
=sinAcosB+cosAsinB=sin（A+B），
又∵在△ABC中，A+B+C=π，∴A+B=π-C，
∴sin（A+B）=sin（π-C）=sinC，又∵
•
=sin2C，
∴sinC=sin2C=2sinCcosC，
∴cosC=
，又0＜C＜π，
∴C=
．
（Ⅱ）由a，c，b成等差数列，2c=a+b，
由
•(
-
)=18，∴
•
=18，即abcosC=18，
由（Ⅰ）知cosC=
，所以ab=36，
由余弦弦定理得c2=a2+b2-2abcosC=（a+b）2-3ab，
∴c2=4c2-3×36，
∴c=6
| m |
| n |
又∵在△ABC中，A+B+C=π，∴A+B=π-C，
∴sin（A+B）=sin（π-C）=sinC，又∵
| m |
| n |
∴sinC=sin2C=2sinCcosC，
∴cosC=
| 1 |
| 2 |
∴C=
| π |
| 3 |
（Ⅱ）由a，c，b成等差数列，2c=a+b，
由
| CA |
| AB |
| AC |
| CA |
| CB |
由（Ⅰ）知cosC=
| 1 |
| 2 |
由余弦弦定理得c2=a2+b2-2abcosC=（a+b）2-3ab，
∴c2=4c2-3×36，
∴c=6
点评：向量与三角函数的综合，向量是工具，是手段，考查的落脚点是三角函数的变换公式、图象与性质，三角形中的正余弦定理．
练习册系列答案
七彩题卡口算应用一点通系列答案
相关题目
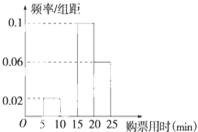某车站在春运期间为了了解旅客购票情况，随机抽样调查了100名旅客从开始在售票窗口排队到购到车票所用的时间t（以下简称为购票用时，单位为min），如图是这次调查统计分析得到的数据（如图所示）．