题目内容
在△ABC中，内角A、B、C的对边分别为a、b、c，已知cos2A-1=
cos（B+C）．
（1）求内角A的大小；
（2）若b=5，△ABC的面积S=5
，求sinBsinC的值．
| 3 |
| 2 |
（1）求内角A的大小；
（2）若b=5，△ABC的面积S=5
| 3 |
考点：解三角形
专题：计算题,解三角形
分析：（1）由cos2A-1=
cos（B+C），可得2cos2A+3cosA-2=0，求得cosA的值，进而求得A．
（2）利用三角形面积公式和已知条件求得c，然后利用余弦定理求得a，进而根据正弦定理求得2R，最后代入sinBsinC的表达式中求得答案．
| 3 |
| 2 |
（2）利用三角形面积公式和已知条件求得c，然后利用余弦定理求得a，进而根据正弦定理求得2R，最后代入sinBsinC的表达式中求得答案．
解答：
解：（1）∵cos2A-1=
cos（B+C），
∴2cos2A+3cosA-2=0，
∴cosA=
，
∴∠A=60°
（2）∵S=
bcsinA=5
∴c=4，
∴a=
=
∵（2R）2=
=28
∴sinBsinC=
=
．
| 3 |
| 2 |
∴2cos2A+3cosA-2=0，
∴cosA=
| 1 |
| 2 |
∴∠A=60°
（2）∵S=
| 1 |
| 2 |
| 3 |
∴c=4，
∴a=
| b2+c2-2bccosA |
| 21 |
∵（2R）2=
| a2 |
| sin2A |
∴sinBsinC=
| bc |
| 4R2 |
| 5 |
| 7 |
点评：本题主要考查了正弦定理和余弦定理的应用．解题的关键是利用正弦定理完成边角问题的转化和化归．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
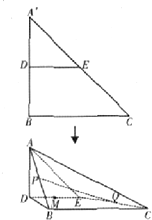如图，在Rt△A′BC中，A′B=BC=2，D，E分别是A′B，A′C的中点，将△A′DE沿线段DE折起到△ADE，使平面ADE⊥平面DBCE．
过x轴上动点A（a，0），引抛物线y=x2+3的两条切线AP、AQ，切点分别为P、Q．
如图所示的几何体为一简单组合体，其底面ABCD为菱形，PD⊥平面ABCD，EC∥PD，且PD=2EC．