题目内容
设函数f(x)=|x+1|+|x+2|+…+|x+2014|+|x-1|+|x-2|+…+|x-2014|(x∈R),四位同学研究得出如下四个命题,其中真命题的有
①f(x)是偶函数;
②f(x)在(0,+∞)单调递增;
③不等式f(x)<2014×2015的解集为∅;
④关于实数a的方程f(2a-3)=f(a-1)可能有无数解.
①f(x)是偶函数;
②f(x)在(0,+∞)单调递增;
③不等式f(x)<2014×2015的解集为∅;
④关于实数a的方程f(2a-3)=f(a-1)可能有无数解.
考点:命题的真假判断与应用
专题:简易逻辑
分析:对于①利用偶函数的定义可判断;对于②正确;对于③研究函数的最小值为2×
=2010×2011,故可判断;对于④当a∈[1,2]时,2a-3∈[-1,1],a-1∈[-1,1],此时方程f(2a-3)=f(a-1)恒成立,故可得结论
| 2014×2015 |
| 2 |
解答:
解:∵f(x)=|x+1|+|x+2|+…+|x+2014|+|x-1|+|x-2|+…+|x-2014|
∴f(-x)=|-x+1|+|-x+2|+…+|-x+2014|+|-x-1|+|-x-2|+…+|-x-2014|=|x+1|+|x+2|+…+|x+2014|+|x-1|+|x-2|+…+|x-2014|=f(x)
∴①f(x)是偶函数,正确;
对于②,当x在[-1,1]的时候,|x+1|+|x-1|就是x到-1的距离加上x到1的距离,由于x在-1和1之间,所以距离之和正好是2,
同样的,|x+2|+|x-2|正好是4,|x+2011|+|x-2011|正好是4022,即函数在[-1,1]上是常数函数,故②错误;
对于③,∵当x=0时,函数的最小值为2×
=2014×2015,故正确;
对于④由②可知,当a∈[1,2]时,2a-3∈[-1,1],a-1∈[-1,1],此时方程f(2a-3)=f(a-1)恒成立,故④正确,
故答案为:①③④
∴f(-x)=|-x+1|+|-x+2|+…+|-x+2014|+|-x-1|+|-x-2|+…+|-x-2014|=|x+1|+|x+2|+…+|x+2014|+|x-1|+|x-2|+…+|x-2014|=f(x)
∴①f(x)是偶函数,正确;
对于②,当x在[-1,1]的时候,|x+1|+|x-1|就是x到-1的距离加上x到1的距离,由于x在-1和1之间,所以距离之和正好是2,
同样的,|x+2|+|x-2|正好是4,|x+2011|+|x-2011|正好是4022,即函数在[-1,1]上是常数函数,故②错误;
对于③,∵当x=0时,函数的最小值为2×
| 2014×2015 |
| 2 |
对于④由②可知,当a∈[1,2]时,2a-3∈[-1,1],a-1∈[-1,1],此时方程f(2a-3)=f(a-1)恒成立,故④正确,
故答案为:①③④
点评:本题主要考查命题真假的判断,解题的关键是正确理解函数,研究其性质.

练习册系列答案
相关题目
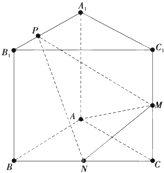 如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,AA1=AB=AC=1,AB⊥AC,M、N分别是CC1,BC的中点,点P在线段A1B1上,且
如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,AA1=AB=AC=1,AB⊥AC,M、N分别是CC1,BC的中点,点P在线段A1B1上,且 在平面直角坐标系中,已知椭圆C:
在平面直角坐标系中,已知椭圆C: 如图,已知椭圆
如图,已知椭圆