题目内容
设数列{an}的首项a1=3，若对于任意的正整数n都有an+1=2an+3．
（1）设bn=an+3，求证：数列{bn}是等比数列；
（2）求数列{an}的通项公式．
（1）设bn=an+3，求证：数列{bn}是等比数列；
（2）求数列{an}的通项公式．
考点：数列递推式,等比关系的确定
专题：点列、递归数列与数学归纳法
分析：（1）把给出的递推式两边同时加3，整理变形后结合bn=an+3证得答案；
（2）由（1）中所证数列{bn}是等比数列，求出等比数列的通项公式，代入bn=an+3求得数列{an}的通项公式．
（2）由（1）中所证数列{bn}是等比数列，求出等比数列的通项公式，代入bn=an+3求得数列{an}的通项公式．
解答：
（1）证明：由an+1=2an+3，得：
an+1+3=2（an+3），
∵a1=3，
∴a1+3=6≠0，
∴
=2，
即
=2．
∴数列{bn}是等比数列；
（2）由数列{bn}是等比数列，
且b1=6，q=2，
得bn=b1qn-1=6•2n-1，
∴an+3=6•2n-1，
则an=6•2n-1-3．
an+1+3=2（an+3），
∵a1=3，
∴a1+3=6≠0，
∴
| an+1+3 |
| an+3 |
即
| bn+1 |
| bn |
∴数列{bn}是等比数列；
（2）由数列{bn}是等比数列，
且b1=6，q=2，
得bn=b1qn-1=6•2n-1，
∴an+3=6•2n-1，
则an=6•2n-1-3．
点评：本题考查了数列递推式，考查了等比关系的确定，训练了等比数列通项公式的求法，是中档题．
练习册系列答案
相关题目
y=2cosx的图象经过怎样的变换能变成函数y=2cos（2x+
）的图象（ ）
| π |
| 3 |
A、向左平移
| ||||
B、向左平移
| ||||
C、将图象上各点的横坐标缩短到原来的
| ||||
D、将图象上各点的横坐标伸长到原来的2倍，纵坐标不变，再向左平移
|
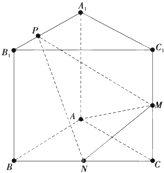如图，已知三棱柱ABC-A1B1C1的侧棱与底面垂直，AA1=AB=AC=1，AB⊥AC，M、N分别是CC1，BC的中点，点P在线段A1B1上，且
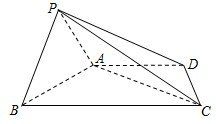如图，四棱锥P-ABCD中，底面ABCD为梯形，AD∥BC，