题目内容
20.已知f(x)=xlnx,其中x∈(0,e](e是自然常数).(Ⅰ)判断函数f(x)的单调性并求出其极小值;
(Ⅱ)若存在x0∈(0,e],使f(x0)≤a,求a的范围.
分析 (Ⅰ)求出函数的导数,解关于导函数的不等式,求出函数的单调区间,从而求出函数的极小值即可;
(Ⅱ)根据函数的单调性得到函数的最小值,从而求出a的范围即可.
解答 解:(Ⅰ)f′(x)=lnx+1,
令f′(x)<0,解得:0<x<$\frac{1}{e}$,
令f′(x)>0,解得:x>$\frac{1}{e}$,
故f(x)在(0,$\frac{1}{e}$)递减,在($\frac{1}{e}$,e]递增;
故f(x)极小值=f($\frac{1}{e}$)=-$\frac{1}{e}$;
(Ⅱ)由(Ⅰ)得:x∈(0,e]时,f(x)min=-$\frac{1}{e}$,
故a≥-$\frac{1}{e}$.
点评 本题考查了函数的单调性、最值问题,考查导数的应用,是一道中档题.

练习册系列答案
相关题目
15.设函数f(x)是定义在(0,+∞)上的可导函数,其导函数为f′(x),f(x)>0恒成立,且有2f(x)>xf′(x)+x,则当x>0时,下列不等关系一定正确的是( )
| A. | 4xf(x2)≤x4f(2x) | B. | e2xf($\frac{1}{x}$)≥$\frac{1}{{x}^{2}}$f(ex) | ||
| C. | xf($\sqrt{x}$)≤f(x) | D. | 4xf(x+1)≤(x2+2x+1)f(2$\sqrt{x}$) |
5.设函数y=f(x)的定义域为D,若对于任意x1,x2∈D,当x1+x2=2a时,恒有f(x1)+f(x2)=2b,则称点(a,b)为函数y=f(x)图象的对称中心.研究函数f(x)=x+sinπx-3的某一个对称中心,并利用对称中心的上述定义,可得到$f(\frac{1}{2017})+f(\frac{2}{2017})+f(\frac{3}{2017})+…+f(\frac{4032}{2017})+f(\frac{4033}{2017})$的值为( )
| A. | -4033 | B. | 4033 | C. | 8066 | D. | -8066 |
9.已知P,A,B是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$上不同的三点,且A,B关于原点对称,若直线PA,PB的斜率乘积${k_{PA}}•{k_{PB}}=\frac{3}{4}$,则该双曲线的离心率是( )
| A. | 2 | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{\sqrt{7}}}{2}$ | D. | $2\sqrt{2}$ |
10.函数$f(x)={2^x}+xln\frac{1}{4}$在区间[-2,2]上的最大值为( )
| A. | $\frac{1}{4}+4ln2$ | B. | 4(1-ln2) | C. | 2(1-ln2) | D. | 4(2ln2-1) |
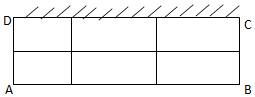 某养猪厂建造一间背面靠墙的长方形猪圈,已知猪圈地面面积为18平方米,将猪圈分割成(如图所示)六个小猪圈,猪圈高度为1米,猪圈每平方米的造价为500元,且不计猪圈背面和地面的费用与猪圈的厚度,问怎样设计总造价最低,最低造价是多少?
某养猪厂建造一间背面靠墙的长方形猪圈,已知猪圈地面面积为18平方米,将猪圈分割成(如图所示)六个小猪圈,猪圈高度为1米,猪圈每平方米的造价为500元,且不计猪圈背面和地面的费用与猪圈的厚度,问怎样设计总造价最低,最低造价是多少?