题目内容
5.设函数y=f(x)的定义域为D,若对于任意x1,x2∈D,当x1+x2=2a时,恒有f(x1)+f(x2)=2b,则称点(a,b)为函数y=f(x)图象的对称中心.研究函数f(x)=x+sinπx-3的某一个对称中心,并利用对称中心的上述定义,可得到$f(\frac{1}{2017})+f(\frac{2}{2017})+f(\frac{3}{2017})+…+f(\frac{4032}{2017})+f(\frac{4033}{2017})$的值为( )| A. | -4033 | B. | 4033 | C. | 8066 | D. | -8066 |
分析 求出f(x)的对称中心,根据函数的对称性计算.
解答 解:f(1)=1-3=-2,
当x1+x2=2时,f(x1)+f(x2)=x1+x2+sinπx1+sinπx2-6=sinπx1+sin(2π-πx1)-4=sinπx1-sinπx1-4=-4,
∴f(x)的对称中心为(1,-2),
∵$\frac{1}{2017}$+$\frac{4033}{2017}$=$\frac{2}{2017}+\frac{4032}{2017}$=…=$\frac{2016}{2017}+\frac{2018}{2017}$=2,
∴$f(\frac{1}{2017})+f(\frac{2}{2017})+f(\frac{3}{2017})+…+f(\frac{4032}{2017})+f(\frac{4033}{2017})$=2016×(-4)+(-2)=-8066.
故选D.
点评 本题考查了函数对称性的应用,属于中档题.

练习册系列答案
相关题目
13.2017年实验中学要给三个班级补发8套教具,先将其分成3堆,其中一堆4个,另两堆每堆2个,一共有多少种不同分堆方法( )
| A. | C${\;}_{8}^{4}$C${\;}_{4}^{2}$C${\;}_{2}^{2}$ | B. | C${\;}_{3}^{1}$C${\;}_{8}^{2}$ | ||
| C. | $\frac{{C}_{8}^{4}{C}_{4}^{2}}{{A}_{2}^{2}}$ | D. | $\frac{{C}_{8}^{4}{C}_{4}^{2}{C}_{2}^{2}}{{A}_{3}^{3}}$ |
14.平行于直线x+2y+1=0,且与圆x2+y2=5相切的直线的方程是( )
| A. | $x+2y+\sqrt{5}=0$或$x+2y-\sqrt{5}=0$ | B. | $x-2y+\sqrt{5}=0$或$x-2y-\sqrt{5}=0$ | ||
| C. | x+2y+5=0或x+2y-5=0 | D. | x-2y+5=0或x-2y-5=0 |
 将全体正整数ai,j从左向右排成一个直角三角形数阵:
将全体正整数ai,j从左向右排成一个直角三角形数阵: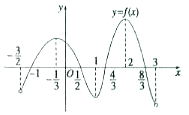 函数y=f(x)在其定义域$[{-\frac{3}{2},3}]$内可导,其图象如图所示,记y=f(x)的导函数为y=f'(x),则不等式f′(x)≤0的解集是[-$\frac{1}{3}$,1]∪[2,3).
函数y=f(x)在其定义域$[{-\frac{3}{2},3}]$内可导,其图象如图所示,记y=f(x)的导函数为y=f'(x),则不等式f′(x)≤0的解集是[-$\frac{1}{3}$,1]∪[2,3).