题目内容
17.已知等式:cos261°+sin231°+cos61°sin31°=a
cos266°+sin236°+cos66°sin36°=a
cos220°+sin210°+cos20°sin(-10°)=a
cos28°+sin222°+cos8°sin(-22°)=a
(Ι)根据以上所给的等式归纳出一个具有一般性的等式,并指出实数a的值
(Ⅱ)证明你写的等式.
分析 (Ι)猜测cos260°+sin2(60°-30°)+cos60°sin(60°-30°)=a,可归纳出一个具有一般性的等式,并指出实数a的值
(Ⅱ)利用公式展开证明等式即可.
解答 解:(Ι)已知等式可化为cos261°+sin2(61°-30°)+cos61°sin(61°-30°)=a,
cos220°+sin2(20°-30°)+cos20°sin(20°-30°)=a,
cos220°+sin2(20°-30°)+cos20°sin(20°-30°)=ac,
os28°+sin2(8°-30°)+cos8°sin(8°-30°)=a
由此猜测cos260°+sin2(60°-30°)+cos60°sin(60°-30°)=a,
∴$a=\frac{3}{4}$-------------------------------------(4分)
即一般性的等式为${cos^2}{α°}+{sin^2}({α°}-{30°})+cos{α°}sin({α°}-{30°})=\frac{3}{4}$------(7分)
(Ⅱ)证明:cos2α°+sin2(α°-30°)+cosα°sin(α°-30°)=${cos^2}{α°}+{(\frac{{\sqrt{3}}}{2}sin{α°}-\frac{1}{2}cos{α°})^2}+cos{α°}(\frac{{\sqrt{3}}}{2}sin{α°}-\frac{1}{2}cos{α°})$----(9分)
=${cos^2}{α°}+\frac{3}{4}{sin^2}{α°}+\frac{1}{4}{cos^2}{α°}-\frac{1}{2}{cos^2}{α°}$
=$\frac{3}{4}{cos^2}{α°}+\frac{3}{4}{sin^2}{α°}$=$\frac{3}{4}$,
∴${cos^2}{α°}+{sin^2}({α°}-{30°})+cos{α°}sin({α°}-{30°})=\frac{3}{4}$--------(12分)
点评 本题考查三角恒等式的证明,考查归纳推理,考查学生分析解决问题的能力,属于中档题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案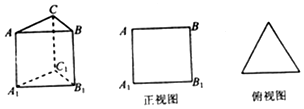 如图所示,水平放置的三棱柱的侧棱长和底面边长均为1,且侧棱A A1⊥面A1 B1C1,正视图是边长为1的正方形,该三棱柱的侧视图面积为( )
如图所示,水平放置的三棱柱的侧棱长和底面边长均为1,且侧棱A A1⊥面A1 B1C1,正视图是边长为1的正方形,该三棱柱的侧视图面积为( )| A. | 3 | B. | $2\sqrt{3}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\sqrt{3}$ |