题目内容
已知x，y∈[-
，
]，a∈R，且有x3+sinx-2a=0，4y3+sinycosy+a=0，则sin（
+4y3）=（ ）
| π |
| 4 |
| π |
| 4 |
| x3 |
| 2 |
| A、-1 | ||
| B、1 | ||
C、
| ||
| D、0 |
考点：同角三角函数基本关系的运用
专题：三角函数的求值
分析：根据两等式变形得到2a=x3+sinx=（-2y）3+sin（-2y），构造函数f（x）=x3+sinx，可得f（x）=f（-2y），利用函数的单调增减性得到x=-2y，代入原式计算即可得到结果．
解答：
解：∵x3+sinx-2a=0，4y3+sinycosy+a=0，
∴2a=x3+sinx=（-2y）3+sin（-2y），
构造函数f（x）=x3+sinx，
∴f（x）=f（-2y），
又∵x，y∈[-
，
]，f′（x）=3x2+cosx≥0，
∴f（x）是增函数，
∴x=-2y，
则sin（
+4y3）=sin0=0．
故选：D．
∴2a=x3+sinx=（-2y）3+sin（-2y），
构造函数f（x）=x3+sinx，
∴f（x）=f（-2y），
又∵x，y∈[-
| π |
| 4 |
| π |
| 4 |
∴f（x）是增函数，
∴x=-2y，
则sin（
| x3 |
| 2 |
故选：D．
点评：此题考查了同角三角函数基本关系的应用，弄清题意是解本题的关键．
练习册系列答案
相关题目
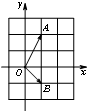如图，在复平面内，若复数z1，z2对应的向量分别是| OA |
| OB |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
已知集合A={-1，0，1}，B={x|x+1＞0}，那么A∩B等于（ ）
| A、{0，1} |
| B、{-1，0，1} |
| C、（-1，+∞） |
| D、[-1，+∞） |
集合A={x|x2+x-6＜0}，B={y|y=lg（x2+1）}，则A∩B等于（ ）
| A、（-3，2） |
| B、[0，3） |
| C、[0，+∞） |
| D、[0，2） |
阅读如图所示的程序框图，运行相应的程序．若输入的x∈[0，2），则输出的结果可能是（ ）
| A、-1 | B、0 | C、1.5 | D、3 |
已知sinα-cosα=
，则cos2（
-α）=（ ）
| 1 |
| 3 |
| π |
| 4 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|