题目内容
已知函数y=f(x)(x∈R)满足f(2x)=2x+1+1,定义数列{an},a1=1,an+1=f(an)-1(n∈N*),数列{bn}的前n项和为Sn,b1=1,且
-
=1(n∈N*).
(1)求数列{an}、{bn}的通项公式;
(2)令cn=
(n∈N+),求{cn}的前n项和Tn;
(3)数列{an}中是否存在三项am,an,ak(m<n<k,m,n,k∈N*)使am,an,ak成等差数列,若存在,求出m,n,k的值,若不存在,请说明理由.
| Sn+1 |
| Sn |
(1)求数列{an}、{bn}的通项公式;
(2)令cn=
| bn |
| an |
(3)数列{an}中是否存在三项am,an,ak(m<n<k,m,n,k∈N*)使am,an,ak成等差数列,若存在,求出m,n,k的值,若不存在,请说明理由.
考点:数列递推式,数列的求和
专题:点列、递归数列与数学归纳法
分析:(1)由f(2x)=2x+1+1求得函数f(x)的解析式,结合an+1=f(an)-1得到数列{an}的递推式,确定数列{an}为等比数列,求得其通项公式,再由
-
=1求出数列{bn}的前n项和,进一步求得数列{bn}的通项公式;
(2)把数列{an}和{bn}的通项公式代入cn=
,利用错位相减法求数列{cn}的前n项和Tn;
(3)假设存在am,an,ak(m<n<k,m,n,k∈N*)使am,an,ak成等差数列,由等差中项的概念得到2n+1-m=1+2k-m,该式不成立,说明假设错误.
| Sn+1 |
| Sn |
(2)把数列{an}和{bn}的通项公式代入cn=
| bn |
| an |
(3)假设存在am,an,ak(m<n<k,m,n,k∈N*)使am,an,ak成等差数列,由等差中项的概念得到2n+1-m=1+2k-m,该式不成立,说明假设错误.
解答:
解:(1)由f(2x)=2x+1+1,得
f(x)=2x+1,又an+1=f(an)-1,
得an+1=2an+1-1=2an,又a1=1,
∴{an}是以1为首项,2为公比的等比数列,
故an=2n-1,
由b1=1,
-
=1(n∈N*),
可得{
}是已1为首项,1为公差的等差数列,
∴
=n,Sn=n2,
则bn=Sn-Sn-1=2n-1(n≥2),
当n=1时,b1=1满足上式,
∴bn=2n-1;
(2)由cn=
,an=2n-1,bn=2n-1得
cn=
,
∴Tn=c1+c2+c3+…+cn,
即Tn=1+
+
+
+…+
①
两边同乘公比
得,
Tn=
+
+
+
+…+
②
①-②得(1-
)Tn=1+
+
+
+
+…+
-
,
化简得:Tn=6-
;
(3)假设存在am,an,ak(m<n<k,m,n,k∈N*)使am,an,ak成等差数列,
则2an=am+ak,
2•2n-1=2m-1+2k-1,
两边同除2m-1,得2n+1-m=1+2k-m,
∵2n+1-m为偶数,而1+2k-m为奇数,上面等式矛盾.
∴假设不成立,
故不存在任三项能构成等差数列.
f(x)=2x+1,又an+1=f(an)-1,
得an+1=2an+1-1=2an,又a1=1,
∴{an}是以1为首项,2为公比的等比数列,
故an=2n-1,
由b1=1,
| Sn+1 |
| Sn |
可得{
| Sn |
∴
| Sn |
则bn=Sn-Sn-1=2n-1(n≥2),
当n=1时,b1=1满足上式,
∴bn=2n-1;
(2)由cn=
| bn |
| an |
cn=
| 2n-1 |
| 2n-1 |
∴Tn=c1+c2+c3+…+cn,
即Tn=1+
| 3 |
| 2 |
| 5 |
| 22 |
| 7 |
| 23 |
| 2n-1 |
| 2n-1 |
两边同乘公比
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 22 |
| 5 |
| 23 |
| 7 |
| 24 |
| 2n-1 |
| 2n |
①-②得(1-
| 1 |
| 2 |
| 2 |
| 2 |
| 2 |
| 22 |
| 2 |
| 23 |
| 2 |
| 24 |
| 2 |
| 2n-1 |
| 2n-1 |
| 2n |
化简得:Tn=6-
| 2n+3 |
| 2n-1 |
(3)假设存在am,an,ak(m<n<k,m,n,k∈N*)使am,an,ak成等差数列,
则2an=am+ak,
2•2n-1=2m-1+2k-1,
两边同除2m-1,得2n+1-m=1+2k-m,
∵2n+1-m为偶数,而1+2k-m为奇数,上面等式矛盾.
∴假设不成立,
故不存在任三项能构成等差数列.
点评:本题考查了数列递推式,考查了等差数列和等比数列的通项公式的求法,训练了利用错位相减法求数列的和,体现了反证法解题思想,是中档题.

练习册系列答案
相关题目
 已知椭圆C:
已知椭圆C: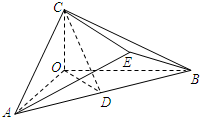 如图,在三棱锥C-OAB中,CO⊥平面AOB,OA=OB=2OC=2,AB=2
如图,在三棱锥C-OAB中,CO⊥平面AOB,OA=OB=2OC=2,AB=2