题目内容
已知函数f(x)=log
(a-2x)+x-2,若f(x)存在零点,则实数a的取值范围是 .
2 |
考点:对数函数的图像与性质,对数的运算性质
专题:函数的性质及应用
分析:根据函数零点与对应方程根之间的关系,将f(x)存在零点转化为方程log2(a-2x)=2-x有根,结合对数方程和指数方程的解法,将它转化为一个二次方程根的存在性,再根据二次方程根的个数与判别式的关系及韦达定理,构造一个关于a的不等式组,解不之即可求出实数a的取值范围.
解答:
解:若f(x)存在零点,
则方程log2(a-2x)=2-x有根
即22-x=a-2x有根,
令2x=t(t>0)
则原方程等价于
=a-t有正根
即t2-at+4=0有正根,
根据根与系数的关系t1t2=4>0,
即若方程有正根,必有两正根,
故有
∴a≥4.
故答案为:a≥4.
则方程log2(a-2x)=2-x有根
即22-x=a-2x有根,
令2x=t(t>0)
则原方程等价于
| 4 |
| t |
即t2-at+4=0有正根,
根据根与系数的关系t1t2=4>0,
即若方程有正根,必有两正根,
故有
|
∴a≥4.
故答案为:a≥4.
点评:本题考查的知识点是函数零点的判定定理,其中根据指数方程和对数方程的解法,将函数对应的方程转化为一个二次方程是解答的关键.体现了换元和转化的数学思想.

练习册系列答案
相关题目
将两个数a=8,b=17交换,使a=17,b=8,下面语句正确的一组是( )
| A、a=b b=a |
| B、b=a a=b |
| C、c=b b=a a=c |
| D、a=c c=b b=a |
已知向量
=(2,-3,5)与向量
=(-4,x,y)平行,则x,y的值分别是( )
| a |
| b |
| A、-6和10 |
| B、6和-10 |
| C、-6和-10 |
| D、6和10 |
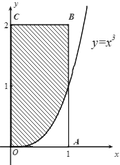 如图所示,在矩形OABC内任取一点P,则点P恰落在图中阴影部分中的概率为
如图所示,在矩形OABC内任取一点P,则点P恰落在图中阴影部分中的概率为