题目内容
17．类比平面几何中的勾股定理：若直角三角形ABC中的两边AB、AC互相垂直，则三角形三边长之间满足关系：AB2+AC2=BC2．若三棱锥A-BCD的三个侧面ABC、ACD、ADB两两互相垂直，则三棱锥的三个侧面积S1，S2，S3与底面积S之间满足的关系为$S_1^2+S_2^2+S_3^2={S^2}$．分析 斜边的平方等于两个直角边的平方和，可类比到空间就是斜面面积的平方等于三个直角面的面积的平方和，边对应着面．
解答 
解：由边对应着面，边长对应着面积，
由类比可得$S_1^2+S_2^2+S_3^2={S^2}$，
故答案为$S_1^2+S_2^2+S_3^2={S^2}$．
点评 本题考查了从平面类比到空间，属于基本类比推理．
练习册系列答案
优生乐园系列答案
相关题目
已知底面为正方形的四棱锥P-ABCD，如图（1）所示，PC⊥面ABCD，其中图（2）为该四棱锥的正（主）视图和侧（左）视图，它们是腰长为4cm的全等的等腰直角三角形．
12．执行如图所示的程序框图，则输出m的值为（ ）
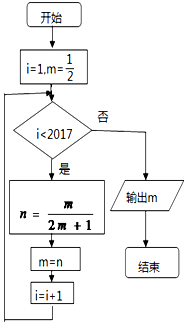
| A． | $\frac{1}{2016}$ | B． | $\frac{1}{2017}$ | C． | $\frac{1}{4032}$ | D． | $\frac{1}{4034}$ |
9．读程序：
则运行程序后输出结果判断正确的是（ ）
则运行程序后输出结果判断正确的是（ ）
| A． | $S=\frac{100}{101}，P=\frac{100}{101}$ | B． | $S=\frac{99}{100}，P=\frac{99}{202}$ | ||
| C． | $S=\frac{100}{101}，P=\frac{99}{202}$ | D． | $S=\frac{100}{101}，P=\frac{99}{100}$ |
6．
如图，已知正方体ABCD-A'B'C'D'的外接球的体积为$\frac{{\sqrt{3}}}{2}π$，将正方体割去部分后，剩余几何体的三视图如图所示，则剩余几何体的表面积为（ ）
如图，已知正方体ABCD-A'B'C'D'的外接球的体积为$\frac{{\sqrt{3}}}{2}π$，将正方体割去部分后，剩余几何体的三视图如图所示，则剩余几何体的表面积为（ ）| A． | $\frac{9}{2}+\frac{{\sqrt{3}}}{2}$ | B． | $3+\sqrt{3}$或$\frac{9}{2}+\frac{{\sqrt{3}}}{2}$ | C． | $2+\sqrt{3}$ | D． | $\frac{9}{2}+\frac{{\sqrt{3}}}{2}$或$2+\sqrt{3}$ |
如图，在三棱锥ABC-A1B1C1中，△ABC是边长为2的等边三角形，AA1=4，A1在底面ABC上的射影为BC的中点E，D是B1C1的中点．