题目内容
6. 如图,已知正方体ABCD-A'B'C'D'的外接球的体积为$\frac{{\sqrt{3}}}{2}π$,将正方体割去部分后,剩余几何体的三视图如图所示,则剩余几何体的表面积为( )
如图,已知正方体ABCD-A'B'C'D'的外接球的体积为$\frac{{\sqrt{3}}}{2}π$,将正方体割去部分后,剩余几何体的三视图如图所示,则剩余几何体的表面积为( )| A. | $\frac{9}{2}+\frac{{\sqrt{3}}}{2}$ | B. | $3+\sqrt{3}$或$\frac{9}{2}+\frac{{\sqrt{3}}}{2}$ | C. | $2+\sqrt{3}$ | D. | $\frac{9}{2}+\frac{{\sqrt{3}}}{2}$或$2+\sqrt{3}$ |
分析 设正方体的棱长为a,则$\frac{4π}{3}(\frac{\sqrt{3}a}{2})^{3}$=$\frac{{\sqrt{3}}}{2}π$,解得a=1.该几何体为正方体截去一角,如图,即可得出.
解答 解:设正方体的棱长为a,则$\frac{4π}{3}(\frac{\sqrt{3}a}{2})^{3}$=$\frac{{\sqrt{3}}}{2}π$,解得a=1.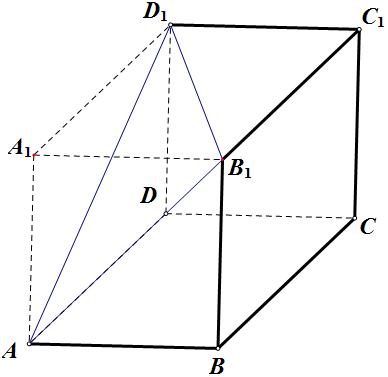
该几何体为正方体截去一角,如图
则剩余几何体的表面积为S=3×12+$\frac{1}{2}×{1}^{2}×3$+$\frac{\sqrt{3}}{4}×(\sqrt{2})^{2}$
=$\frac{9+\sqrt{3}}{2}$.
故选:A.
点评 本题考查了正方体的三视图及其表面积计算公式,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
18.下面几种推理过程是演绎推理的是( )
| A. | 某校高三有8个班,1班有51人,2班有53人,3班有52人,由此推测各班人数都超过50人 | |
| B. | 由三角形的性质,推测空间四面体的性质 | |
| C. | 平行四边形的对角线互相平分,菱形是平行四边形,所以菱形的对角线互相平分 | |
| D. | 在数列{an}中,a1=1,an=$\frac{1}{2}$(an-1+$\frac{1}{{a}_{n}-1}$),由此归纳出{an}的通项公式 |
15.如图所示,某人拨通了电话,准备手机充值须如下操作( )
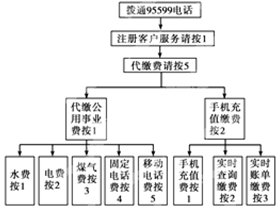

| A. | 1511 | B. | 1515 | C. | 1521 | D. | 1523 |
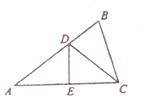 如图,设△ABC的三个内角A,B,C对应的三条边分别为a,b,c,且角A,B,C成等差数列,a=2,线段AC的垂直平分线分别交线段AB,AC于D,E两点.
如图,设△ABC的三个内角A,B,C对应的三条边分别为a,b,c,且角A,B,C成等差数列,a=2,线段AC的垂直平分线分别交线段AB,AC于D,E两点.