题目内容
8.如图,在四边形ABCD中,∠A=90°,AB=AD=2,CB=CD=3,将△ABD沿BD折起,得到三棱锥A'-BDC,O为BD的中点,M为OC的中点,点N在线段A'B上,满足$A'N=\frac{1}{4}A'B$.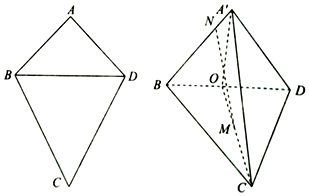
(Ⅰ)证明:MN∥平面A'CD;
(Ⅱ)若A'C=3,求点B到平面A'CD的距离.
分析 (Ⅰ)过点N作BD的平行线,交直线A'D于点E,证明:四边形MNEF为平行四边形,可得MN∥EF,即可证明MN∥平面A'CD;
(Ⅱ)若A'C=3,利用等体积方法,即可求点B到平面A'CD的距离.
解答 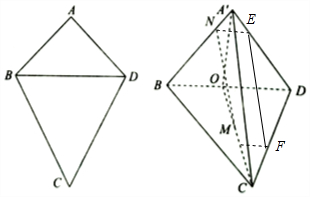 (Ⅰ)证明:过点N作BD的平行线,交直线A'D于点E,
(Ⅰ)证明:过点N作BD的平行线,交直线A'D于点E,
过点M作BD的平行线,交直线CD于点F,…(1分)
因为NE∥BD,MF∥BD,所以NE∥MF,
且$NE=MF=\frac{1}{4}BD$,所以四边形MNEF为平行四边形,…(3分)
所以MN∥EF,且EF?平面A'CD,MN?平面A'CD,
所以MN∥平面A'CD.…(4分)
(Ⅱ)解:因为A'C=3,所以A'O⊥OC,且A'O⊥BD,OC∩BD=O,所以A'O⊥平面BCD.…(6分)
由:VB-A'CD=VA'-BCD${S_{A'CD}}=\frac{1}{2}×2×2\sqrt{2}=2\sqrt{2}$,…(8分)
${S_{BCD}}=\frac{1}{2}×2\sqrt{2}×\sqrt{7}=\sqrt{14}$,$A'O=\sqrt{2}$,…(10分)
所求点B到平面A'CD的距离$h=\frac{{\sqrt{14}×\sqrt{2}}}{{2\sqrt{2}}}=\frac{{\sqrt{14}}}{2}$.…(12分)
点评 本题考查线面平行的判定,考查点到平面距离的计算,考查体积的计算,属于中档题.

练习册系列答案
相关题目
18.下列说法正确的是( )
| A. | 若“x=$\frac{π}{4}$,则tanx=1”的逆命题为真命题 | |
| B. | 在△ABC中,sinA>sinB的充要条件是A>B | |
| C. | 函数f(x)=sinx+$\frac{4}{sinx}$,x∈(0,π)的最小值为4 | |
| D. | ?x∈R,使得sinx•cosx=$\frac{3}{5}$ |
16.设集合A={m∈Z|m≤-3或m≥2},B={n∈N|-1≤n<3},则B∩(∁ZA)=( )
| A. | {0,1,2} | B. | {-1,0,1} | C. | {0,1} | D. | {-1,0,1,2} |
3.已知实数a,b满足(a+bi)(2+i)=3-5i(其中i为虚数单位),则复数z=b-ai的共扼复数为( )
| A. | -$\frac{13}{5}$+$\frac{1}{5}$i | B. | -$\frac{13}{5}$-$\frac{1}{5}$i | C. | $\frac{13}{5}$+$\frac{1}{5}$i | D. | $\frac{13}{5}$-$\frac{1}{5}$i |
20.若$\overrightarrow{a}$=(a1,a2),$\overrightarrow{b}$=(b1,b2),定义一种向量积:$\overrightarrow{a}$?$\overrightarrow{b}$=(a1b1,a2b2),已知$\vec m=(1,\frac{1}{2}),\vec n=(0,1)$,且点P(x,y)在函数$y=sin\frac{x}{2}$的图象上运动,点q在函数y=f(x)的图象上运动,且点p和点q满足:$\overrightarrow{OQ}$=$\overrightarrow{m}$?$\overrightarrow{OP}$+$\overrightarrow{n}$(其中O为坐标原点),则函数y=f(x)的最大值A及最小正周期T分别为( )
| A. | 1,π | B. | 1,4π | C. | $\frac{3}{2},π$ | D. | $\frac{3}{2},4π$ |
17.某校1000名学生中,O型血有400人,A型血有250人,B型血有250人,AB型血有100人,为了研究血型与色弱的关系,要从中抽取一个容量为40的样本,按照分层抽样的方法抽取样本,则O型血、A型血、B型血、AB型血的人要分别抽的人数为( )
| A. | 16、10、10、4 | B. | 14、10、10、6 | C. | 13、12、12、3 | D. | 15、8、8、9 |
8.已知a为常数,函数f(x)=ax3-3ax2-(x-3)ex+1在(0,2)内有两个极值点,则实数a的取值范围为( )
| A. | $(-∞,\frac{e}{3})$ | B. | $(\frac{e}{3},{e^2})$ | C. | $(\frac{e}{3},\frac{e^2}{6})$ | D. | $(\frac{e}{3},+∞)$ |