题目内容
17.某校1000名学生中,O型血有400人,A型血有250人,B型血有250人,AB型血有100人,为了研究血型与色弱的关系,要从中抽取一个容量为40的样本,按照分层抽样的方法抽取样本,则O型血、A型血、B型血、AB型血的人要分别抽的人数为( )| A. | 16、10、10、4 | B. | 14、10、10、6 | C. | 13、12、12、3 | D. | 15、8、8、9 |
分析 由题意,采用分层抽样,可以知道每个个体被抽到的概率,求出抽样比,即可得到结果.
解答 解:根据题意知用分层抽样方法抽样,抽样比为$\frac{40}{1000}$=$\frac{1}{25}$,
故O型血、A型血、B型血、AB型血的人要分别抽的人数为400×$\frac{1}{25}$=16,250×$\frac{1}{25}$=10,250×$\frac{1}{25}$=10,100×$\frac{1}{25}$═4
故选A.
点评 本题考查分层抽样,抽样过程中每个个体被抽到的可能性相同,这是解决抽样问题的依据,样本容量、总体个数、每个个体被抽到的概率,这三者可以做到知二求一.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
12.复数z满足z(1+i)=|1-i|,则复数z的虚部是( )
| A. | -1 | B. | 1 | C. | -$\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
2.抛物线y=$\frac{1}{4}$x2的准线方程是( )
| A. | y=-1 | B. | y=1 | C. | x=-$\frac{1}{16}$ | D. | x=$\frac{1}{16}$ |
9.曲线C的参数方程为$\left\{{\begin{array}{l}{x=4cosα}\\{y=sinα}\end{array}}\right.$(α为参数),M是曲线C上的动点,若曲线T极坐标方程2ρsinθ+ρcosθ=20,则点M到T的距离的最大值( )
| A. | $\sqrt{13}+4\sqrt{5}$ | B. | $2+4\sqrt{5}$ | C. | $4+4\sqrt{5}$ | D. | $6\sqrt{5}$ |
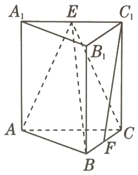 如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AB⊥BC,AA1=AC=2,BC=1,E,F分别为A1C1,BC的中点.
如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AB⊥BC,AA1=AC=2,BC=1,E,F分别为A1C1,BC的中点.