题目内容
19.下列条件:(1)ab>0,(2)ab<0,(3)a>0,b>0,(4)a<0,b<0,其中能使$\frac{b}{a}+\frac{a}{b}≥2$成立的条件的个数是3.分析 当a,b同号时,$\frac{b}{a}>0,\frac{a}{b}>0$,$\frac{b}{a}+\frac{a}{b}≥2$,进而得到答案.
解答 解:当a,b同号时,$\frac{b}{a}>0,\frac{a}{b}>0$,$\frac{b}{a}+\frac{a}{b}≥2$,
故:(1)ab>0,(3)a>0,b>0,(4)a<0,b<0,能使$\frac{b}{a}+\frac{a}{b}≥2$成立,
故答案为:3
点评 本题以命题的真假判断与应用为载体,考查了基本不等式,难度基础.

练习册系列答案
相关题目
10.设全集U=R,集合A={x|x2-1<0},B={x|x(x-3)>0}则A∩(∁UB)=( )
| A. | {x|0<x<2} | B. | {x|0<x<1} | C. | {x|0≤x<1} | D. | {x|-1<x<0} |
4.已知$\overrightarrow{a}$,$\overrightarrow{b}$是两个向量,|$\overrightarrow{a}$|=1,|$\overrightarrow{b}$|=2,且($\overrightarrow{a}$+$\overrightarrow{b}$)⊥$\overrightarrow{a}$,若在△ABC中,$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,D为BC中点,则AD的长为( )
| A. | $\frac{{\sqrt{7}}}{2}$ | B. | $\frac{{\sqrt{6}}}{2}$ | C. | $\frac{{\sqrt{5}}}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
9.曲线C的参数方程为$\left\{{\begin{array}{l}{x=4cosα}\\{y=sinα}\end{array}}\right.$(α为参数),M是曲线C上的动点,若曲线T极坐标方程2ρsinθ+ρcosθ=20,则点M到T的距离的最大值( )
| A. | $\sqrt{13}+4\sqrt{5}$ | B. | $2+4\sqrt{5}$ | C. | $4+4\sqrt{5}$ | D. | $6\sqrt{5}$ |
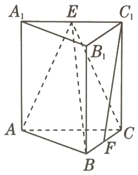 如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AB⊥BC,AA1=AC=2,BC=1,E,F分别为A1C1,BC的中点.
如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AB⊥BC,AA1=AC=2,BC=1,E,F分别为A1C1,BC的中点.