题目内容
18.已知复数z满足iz=|3+4i|-i,则z的虚部是( )| A. | ?-5 | B. | ?-1 | C. | ?-5i | D. | ?-i |
分析 利用了复数的运算法则、共轭复数与虚部的定义即可得出.
解答 解:复数z满足iz=|3+4i|-i,
∴-i•iz=-i(5-i),
∴z=-1-5i,
则z的虚部是-5.
故选:A.
点评 本题考查了复数的运算法则、共轭复数与虚部的定义,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
9.已知集合A={x||x-1|≤2},B={x|x=2n-1,n∈Z},则A∩B=( )
| A. | {1,3} | B. | {0,2} | C. | {1} | D. | {-1,1,3} |
6.已知$\overrightarrow{a}$、$\overrightarrow{b}$是平面向量,如果|$\overrightarrow{a}$|=3,|$\overrightarrow{b}$|=4,|$\overrightarrow{a}$+$\overrightarrow{b}$|=2,那么|$\overrightarrow{a}$-$\overrightarrow{b}$|=( )
| A. | $\sqrt{46}$ | B. | 7 | C. | 5 | D. | $\sqrt{21}$ |
3.已知函数f(x)=alnx-ax-3(a∈R).若函数y=f(x)的图象在点(2,f(2))处切线的倾斜角为$\frac{π}{4}$,对于任意t∈[1,2]函数g(x)=x3+x2[f′(x)+$\frac{m}{2}$]在区间(t,3)上总不是单调函数,则实数 m 的取值范围是( )
| A. | ?(-∞,-5)? | B. | ?(-$\frac{37}{3}$,-5)? | C. | (-9,+∞)?? | D. | (-$\frac{37}{3}$,-9)? |
10.某校高三年级有男生220人,学籍编号1,2,…,220;女生380人,学籍编号221,222,…,600.为了解学生学习的心理状态,按学籍编号采用系统抽样的方法从这600名学生中抽取10人进行问卷调查(第一组采用简单随机抽样,抽到的号码为10),然后再从这10位学生中随机抽取3人座谈,则3人中既有男生又有女生的概率是( )
| A. | $\frac{1}{5}$ | B. | $\frac{3}{10}$ | C. | $\frac{7}{10}$ | D. | $\frac{4}{5}$ |
7.已知椭圆的左焦点为F1,有一小球A从F1处以速度v开始沿直线运动,经椭圆壁反射(无论经过几次反射速度大小始终保持不变,小球半径忽略不计),若小球第一次回到F1时,它所用的最长时间是最短时间的5倍,则椭圆的离心率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{\sqrt{5}-1}{2}$ | C. | $\frac{3}{5}$ | D. | $\frac{2}{3}$ |
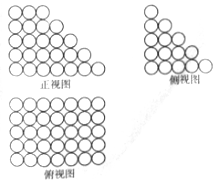 北宋数学家沈括的主要数学成就之一为隙积术,所谓隙积,即“积之有隙”者,如累棋、层坛之类,这种长方台形状的物体垛积,设隙积共n层,上底由a×b个物体组成,以下各层的长、宽依次各增加一个物体,最下层(即下底)由c×d个物体组成,沈括给出求隙积中物体总数的公式为S=$\frac{n}{6}$[(2b+d)a+(b+2d)c]+$\frac{n}{6}$(c-a).已知由若干个相同小球粘黏组成的几何体垛积的三视图如图所示,则该垛积中所有小球的个数为( )
北宋数学家沈括的主要数学成就之一为隙积术,所谓隙积,即“积之有隙”者,如累棋、层坛之类,这种长方台形状的物体垛积,设隙积共n层,上底由a×b个物体组成,以下各层的长、宽依次各增加一个物体,最下层(即下底)由c×d个物体组成,沈括给出求隙积中物体总数的公式为S=$\frac{n}{6}$[(2b+d)a+(b+2d)c]+$\frac{n}{6}$(c-a).已知由若干个相同小球粘黏组成的几何体垛积的三视图如图所示,则该垛积中所有小球的个数为( )