题目内容
7.已知椭圆的左焦点为F1,有一小球A从F1处以速度v开始沿直线运动,经椭圆壁反射(无论经过几次反射速度大小始终保持不变,小球半径忽略不计),若小球第一次回到F1时,它所用的最长时间是最短时间的5倍,则椭圆的离心率为( )| A. | $\frac{1}{3}$ | B. | $\frac{\sqrt{5}-1}{2}$ | C. | $\frac{3}{5}$ | D. | $\frac{2}{3}$ |
分析 由题意可得4a=10(a-c),由此即可求得椭圆的离心率.
解答 解:假设长轴在x轴,短轴在y轴,以下分为三种情况:
(1)球从F1沿x轴向左直线运动,碰到左顶点必然原路反弹,这时第一次回到F1路程是2(a-c);
(2 )球从F1沿x轴向右直线运动,碰到右顶点必然原路反弹,这时第一次回到F1路程是2(a+c);
(3)球从F1沿x轴斜向上(或向下)运动,碰到椭圆上的点A,反弹后经过椭圆的另一个焦点F2,再弹到椭圆上一点B,经F1反弹后经过点F1,此时小球经过的路程是4a.
综上所述,从点F1沿直线出发,经椭圆壁反射后第一次回到点F1时,小球经过的最大路程是4a最小路程是2(a-c).
∴由题意可得4a=10(a-c),即6a=10c,得$\frac{c}{a}=\frac{3}{5}$.
∴椭圆的离心率为$\frac{3}{5}$.
故选:C.
点评 本题考查椭圆的简单性质,明确椭圆上的点到左焦点距离最小的点是左顶点,距离最大的点是右顶点是关键,是基础题.

练习册系列答案
相关题目
17.已知甲、乙两组数据的茎叶图如图所示,若它们的中位数相同,则甲组数据的平均数为( )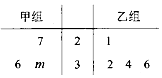

| A. | 32 | B. | 33 | C. | 34 | D. | 35 |
18.已知复数z满足iz=|3+4i|-i,则z的虚部是( )
| A. | ?-5 | B. | ?-1 | C. | ?-5i | D. | ?-i |
2.设P={x|x<4},Q={x|x2<4},则( )
| A. | P⊆Q | B. | Q⊆P | C. | P⊆∁RQ | D. | Q⊆∁RP |
12.已知a>0,且a≠1,若ab>1,则( )
| A. | ab>b | B. | ab<b | C. | a>b | D. | a<b |