题目内容
10.某校高三年级有男生220人,学籍编号1,2,…,220;女生380人,学籍编号221,222,…,600.为了解学生学习的心理状态,按学籍编号采用系统抽样的方法从这600名学生中抽取10人进行问卷调查(第一组采用简单随机抽样,抽到的号码为10),然后再从这10位学生中随机抽取3人座谈,则3人中既有男生又有女生的概率是( )| A. | $\frac{1}{5}$ | B. | $\frac{3}{10}$ | C. | $\frac{7}{10}$ | D. | $\frac{4}{5}$ |
分析 由题意,得到抽到的10人中,有男生4人,女生6人,再从这10位学生中随机抽取3人座谈,基本事件总数n=C${\;}_{10}^{3}$,3人中既有男生又有女生包含的基本事件个数m=${C}_{10}^{3}-{C}_{4}^{3}-{C}_{6}^{3}$,由此能求出3人中既有男生又有女生的概率.
解答 解:由题意,得到抽到的10人中,有男生4人,女生6人,
再从这10位学生中随机抽取3人座谈,
基本事件总数n=C${\;}_{10}^{3}$=120,
3人中既有男生又有女生包含的基本事件个数m=${C}_{10}^{3}-{C}_{4}^{3}-{C}_{6}^{3}$=120-4-20=96,
3人中既有男生又有女生的概率p=$\frac{m}{n}=\frac{96}{120}$=$\frac{4}{5}$.
故选:D.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意等可能事件概率计算公式的合理运用.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
20.已知等差数列{an}满足:a2=2,Sn-Sn-3=54(n>3),Sn=100,则n=( )
| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
1.已知数列{an}、{bn}、{cn},以下两个命题:
①若{an+bn}、{bn+cn}、{an+cn}都是递增数列,则{an}、{bn}、{cn}都是递增数列;
②若{an+bn}、{bn+cn}、{an+cn}都是等差数列,则{an}、{bn}、{cn}都是等差数列;
下列判断正确的是( )
①若{an+bn}、{bn+cn}、{an+cn}都是递增数列,则{an}、{bn}、{cn}都是递增数列;
②若{an+bn}、{bn+cn}、{an+cn}都是等差数列,则{an}、{bn}、{cn}都是等差数列;
下列判断正确的是( )
| A. | ①②都是真命题 | B. | ①②都是假命题 | ||
| C. | ①是真命题,②是假命题 | D. | ①是假命题,②是真命题 |
18.已知复数z满足iz=|3+4i|-i,则z的虚部是( )
| A. | ?-5 | B. | ?-1 | C. | ?-5i | D. | ?-i |
5.已知复数$z=\frac{a+i}{1-i}$(其中i为虚数单位),若z为纯虚数,则实数a等于( )
| A. | -1 | B. | 0 | C. | 1 | D. | $\sqrt{2}$ |
2.设P={x|x<4},Q={x|x2<4},则( )
| A. | P⊆Q | B. | Q⊆P | C. | P⊆∁RQ | D. | Q⊆∁RP |
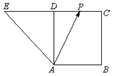 如图,四边形ABCD是正方形,延长CD至E,使得DE=CD,若点P为CD的中点,且$\overrightarrow{AP}=λ\overrightarrow{AB}+μ\overrightarrow{AE}$,则λ+μ=( )
如图,四边形ABCD是正方形,延长CD至E,使得DE=CD,若点P为CD的中点,且$\overrightarrow{AP}=λ\overrightarrow{AB}+μ\overrightarrow{AE}$,则λ+μ=( )