题目内容
9.已知集合A={x||x-1|≤2},B={x|x=2n-1,n∈Z},则A∩B=( )| A. | {1,3} | B. | {0,2} | C. | {1} | D. | {-1,1,3} |
分析 由绝对值不等式的解法求出A,由条件和交集的运算求出A∩B.
解答 解:由题意知,A={x||x-1|≤2}={x|-1≤x≤3}=[-1,3],
又B={x|x=2n-1,n∈Z}是奇数集,
则A∩B={-1,1,3},
故选D.
点评 本题考查交集及其运算,以及绝对值不等式的解法,属于基础题.

练习册系列答案
相关题目
19.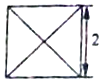 已知某几何体的俯视图是如图所示的边长为2的正方形,主视图与左视图是边长为2的正三角形,则其侧面积( )
已知某几何体的俯视图是如图所示的边长为2的正方形,主视图与左视图是边长为2的正三角形,则其侧面积( )
 已知某几何体的俯视图是如图所示的边长为2的正方形,主视图与左视图是边长为2的正三角形,则其侧面积( )
已知某几何体的俯视图是如图所示的边长为2的正方形,主视图与左视图是边长为2的正三角形,则其侧面积( )| A. | 4 | B. | $4\sqrt{3}$ | C. | $4(1+\sqrt{3})$ | D. | 8 |
20.已知等差数列{an}满足:a2=2,Sn-Sn-3=54(n>3),Sn=100,则n=( )
| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
17.已知甲、乙两组数据的茎叶图如图所示,若它们的中位数相同,则甲组数据的平均数为( )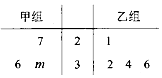

| A. | 32 | B. | 33 | C. | 34 | D. | 35 |
4.以双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)上一点M为圆心作圆,该圆与x轴相切于C的一个焦点F,与y轴交于P,Q两点,若△MPQ为正三角形,则C的离心率等于( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{5}$ |
14.执行如图所示的程序框图,若输入n=10,则输出S=( )
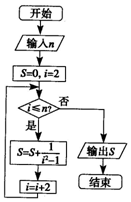

| A. | $\frac{4}{9}$ | B. | $\frac{5}{11}$ | C. | $\frac{6}{13}$ | D. | $\frac{36}{55}$ |
1.已知数列{an}、{bn}、{cn},以下两个命题:
①若{an+bn}、{bn+cn}、{an+cn}都是递增数列,则{an}、{bn}、{cn}都是递增数列;
②若{an+bn}、{bn+cn}、{an+cn}都是等差数列,则{an}、{bn}、{cn}都是等差数列;
下列判断正确的是( )
①若{an+bn}、{bn+cn}、{an+cn}都是递增数列,则{an}、{bn}、{cn}都是递增数列;
②若{an+bn}、{bn+cn}、{an+cn}都是等差数列,则{an}、{bn}、{cn}都是等差数列;
下列判断正确的是( )
| A. | ①②都是真命题 | B. | ①②都是假命题 | ||
| C. | ①是真命题,②是假命题 | D. | ①是假命题,②是真命题 |
18.已知复数z满足iz=|3+4i|-i,则z的虚部是( )
| A. | ?-5 | B. | ?-1 | C. | ?-5i | D. | ?-i |