题目内容
3.已知函数f(x)=alnx-ax-3(a∈R).若函数y=f(x)的图象在点(2,f(2))处切线的倾斜角为$\frac{π}{4}$,对于任意t∈[1,2]函数g(x)=x3+x2[f′(x)+$\frac{m}{2}$]在区间(t,3)上总不是单调函数,则实数 m 的取值范围是( )| A. | ?(-∞,-5)? | B. | ?(-$\frac{37}{3}$,-5)? | C. | (-9,+∞)?? | D. | (-$\frac{37}{3}$,-9)? |
分析 求出函数的导数,利用切线的斜率求出a,利用函数的单调性,任意t∈[1,2]函数g(x)=x3+x2[f′(x)+$\frac{m}{2}$]在区间(t,3)上总不是单调函数,转化为函数由极值,然后求解函数的值域即可得到结果.
解答 解:由函数f(x)=alnx-ax-3(a∈R).可得f′(x)=$\frac{a}{x}$-a,
$f'(2)=-\frac{a}{2}=1$得a=-2,对于任意t∈[1,2]函数$g(x)={x^3}+{x^2}[{f'(x)+\frac{m}{2}}]$=x3+x2(-$\frac{2}{x}$+2+$\frac{m}{2}$)
在区间(t,3)上总不是单调函数,只需$g(x)={x^3}+(\frac{m}{2}+2){x^2}-x$2在(2,3)上不是单调函数,
故g'(x)=3x2+(m+4)x-2在(2,3)上有零点,即方程$m=-3x-4+\frac{2}{x}$在(2,3)上有解,
而$y=-3x-4+\frac{2}{x}$在(2,3)上单调递减,故其值域为$({-\frac{37}{3},-9})$.
故选:D.
点评 本题考查函数的导数的应用,函数的极值以及函数的单调性的判断,考查转化思想以及计算能力.

练习册系列答案
相关题目
13.已知四棱锥P-ABCD的顶点都在球O的球面上,底面ABCD是矩形,平面PAD⊥底面ABCD,△PAD为正三角形,AB=2AD=4,则球O的表面积为( )
| A. | $\frac{56π}{3}$ | B. | $\frac{64π}{3}$ | C. | 24π | D. | $\frac{80π}{3}$ |
14.执行如图所示的程序框图,若输入n=10,则输出S=( )
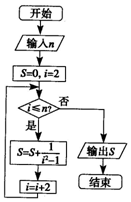

| A. | $\frac{4}{9}$ | B. | $\frac{5}{11}$ | C. | $\frac{6}{13}$ | D. | $\frac{36}{55}$ |
11.已知常数ω>0,f(x)=-1+2$\sqrt{3}$sinωxcosωx+2cos2ωx图象的对称中心得到对称轴的距离的最小值为$\frac{π}{4}$,若f(x0)=$\frac{6}{5}$,$\frac{π}{4}$≤x0≤$\frac{π}{2}$,则cos2x0=( )
| A. | $\frac{3+2\sqrt{3}}{10}$ | B. | $\frac{3-2\sqrt{2}}{10}$ | C. | $\frac{3+4\sqrt{3}}{10}$ | D. | $\frac{3-4\sqrt{3}}{10}$ |
18.已知复数z满足iz=|3+4i|-i,则z的虚部是( )
| A. | ?-5 | B. | ?-1 | C. | ?-5i | D. | ?-i |
8.已知平面α⊥平面β,α∩β=l,直线m?α,直线n?β,且m⊥n,有以下四个结论:
①若n∥l,则m⊥β
②若m⊥β,则n∥l
③m⊥β和n⊥α同时成立
④m⊥β和n⊥α中至少有一个成立
其中正确的是( )
①若n∥l,则m⊥β
②若m⊥β,则n∥l
③m⊥β和n⊥α同时成立
④m⊥β和n⊥α中至少有一个成立
其中正确的是( )
| A. | ①③ | B. | ①④ | C. | ②③ | D. | ②④ |
12.已知a>0,且a≠1,若ab>1,则( )
| A. | ab>b | B. | ab<b | C. | a>b | D. | a<b |