题目内容
 座落于我市红梅公园边的天宁宝塔堪称中华之最,也堪称佛塔世界之最.如图,已知天宁宝塔AB高度为150米,某大楼CD高度为90米,从大楼CD顶部C看天宁宝塔AB的张角∠ACB=45°,求天宁宝塔AB与大楼CD底部之间的距离BD.
座落于我市红梅公园边的天宁宝塔堪称中华之最,也堪称佛塔世界之最.如图,已知天宁宝塔AB高度为150米,某大楼CD高度为90米,从大楼CD顶部C看天宁宝塔AB的张角∠ACB=45°,求天宁宝塔AB与大楼CD底部之间的距离BD.考点:解三角形的实际应用
专题:应用题,解三角形
分析:作CE⊥AB于E,问题转化为求△ACB边AB上的高.设CE=x,只要建立起关于x的方程,则问题可解.
解答:
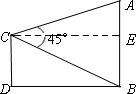 解:如图作CE⊥AB于E.
解:如图作CE⊥AB于E.
∵AB∥CD,AB=150,CD=90,∴BE=90,AE=60.
设CE=x,∠ACE=α,
∵∠ACB=45°,∴∠BCE=45°-α.
在Rt△AEC和Rt△BEC中,
∵tanα=
,tan(45°-α)=
∴
=tan(45°-α)=
,
化简整理得x2-150x-5400=0,
解得x1=180,x2=-30(舍去).
答:两建筑物底部间距离BD是180米.
 解:如图作CE⊥AB于E.
解:如图作CE⊥AB于E.∵AB∥CD,AB=150,CD=90,∴BE=90,AE=60.
设CE=x,∠ACE=α,
∵∠ACB=45°,∴∠BCE=45°-α.
在Rt△AEC和Rt△BEC中,
∵tanα=
| 60 |
| x |
| 90 |
| x |
∴
| 90 |
| x |
1-
| ||
1+
|
化简整理得x2-150x-5400=0,
解得x1=180,x2=-30(舍去).
答:两建筑物底部间距离BD是180米.
点评:本题主要考查了解三角形的实际应用.解这类题的关键是建立数学模型,设出恰当的角

练习册系列答案
相关题目
已知扇形AOB的周长为8cm,面积为3cm2,则其圆心角为( )
A、6或
| ||||
B、6或
| ||||
C、
| ||||
D、
|
若直线(a+2)x+(1-a)y=a2(a>0)与直线(a-1)x+(2a+3)y+2=0互相垂直,则a等于( )
| A、1 | B、-1 | C、±1 | D、-2 |
 在2010年的人口普查中,某市人中普查办公室为召开普查工作意见反馈会,用分层抽样的方法,从某住宅小区中抽取A、B、C、D四个年龄段的居民共50人.如图是该小区这四个年龄段的人数条形图.
在2010年的人口普查中,某市人中普查办公室为召开普查工作意见反馈会,用分层抽样的方法,从某住宅小区中抽取A、B、C、D四个年龄段的居民共50人.如图是该小区这四个年龄段的人数条形图.