题目内容
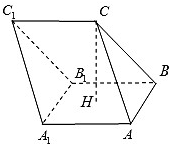 如图,在三棱柱ABC-A1B1C1中,H是正方形AA1B1B的中心,AA1=2,CH⊥平面AA1B1B,且CH=3.
如图,在三棱柱ABC-A1B1C1中,H是正方形AA1B1B的中心,AA1=2,CH⊥平面AA1B1B,且CH=3.(1)求A1C与平面ABC所成角的正弦值;
(2)在线段A1B1上是否存在一点P,使得平面PBC⊥平面ABC?若存在,求出B1P的长;若不存在,说明理由.
考点:直线与平面所成的角,平面与平面垂直的性质
专题:空间位置关系与距离,空间角
分析:(1)建立空间直角坐标系,求出平面ABC的一个法向量,利用向量的夹角公式,即可求出A1C与平面ABC所成角的正弦值;
(2)假设存在点P,则P(λ,0,0),且λ∈[0,2],求出平面PBC的法向量,利用平面PBC⊥平面ABC,可得方程,即可得出结论.
(2)假设存在点P,则P(λ,0,0),且λ∈[0,2],求出平面PBC的法向量,利用平面PBC⊥平面ABC,可得方程,即可得出结论.
解答:
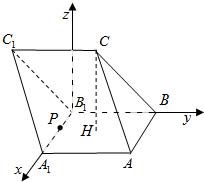 解:如图,以点B1为坐标在原点建立空间直角坐标系,
解:如图,以点B1为坐标在原点建立空间直角坐标系,
则B1(0,0,0),A1(2,0,0),A(2,2,0),B(0,2,0),C(1,1,3)
(1)∵
=(-2,0,0),
=(-1,-1,3).
设平面ABC的一个法向量
=(x,y,z),
则
,即
,
令z=1,得
=(0,3,1)
设A1C与平面ABC所成角为θ,则
∵
=(-1,1,3),
∴sinθ=|
|=
(2)假设存在点P,则P(λ,0,0),且λ∈[0,2],
∴
=(-λ,2,0),
=(1,-1,3).
设平面PBC的法向量
=(x,y,z),
则
,即
,
令x=1,得
=(1,
,
-
).
∵平面PBC⊥平面ABC,∴
⊥
,
即0=
•
=
λ+
-
,得λ=
∈[0,2],
∴存在这样的点P(
,0,0)使得平面PBC⊥平面ABC,且B1P=
.
 解:如图,以点B1为坐标在原点建立空间直角坐标系,
解:如图,以点B1为坐标在原点建立空间直角坐标系,则B1(0,0,0),A1(2,0,0),A(2,2,0),B(0,2,0),C(1,1,3)
(1)∵
| AB |
| AC |
设平面ABC的一个法向量
| n |
则
|
|
令z=1,得
| n |
设A1C与平面ABC所成角为θ,则
∵
| A1C |
∴sinθ=|
| ||||
|
|
| 3 |
| 55 |
| 110 |
(2)假设存在点P,则P(λ,0,0),且λ∈[0,2],
∴
| PB |
| BC |
设平面PBC的法向量
| m |
则
|
|
令x=1,得
| m |
| λ |
| 2 |
| λ |
| 6 |
| 1 |
| 3 |
∵平面PBC⊥平面ABC,∴
| m |
| n |
即0=
| m |
| n |
| 3 |
| 2 |
| λ |
| 6 |
| 1 |
| 3 |
| 1 |
| 5 |
∴存在这样的点P(
| 1 |
| 5 |
| 1 |
| 5 |
点评:本题考查线面角,考查面面垂直,考查空间向量知识的运用,正确求平面的法向量是关键.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
若直线(a+2)x+(1-a)y=a2(a>0)与直线(a-1)x+(2a+3)y+2=0互相垂直,则a等于( )
| A、1 | B、-1 | C、±1 | D、-2 |
把89化这二进制数,其结果为( )
| A、1001101 |
| B、1100101 |
| C、1011011 |
| D、1011001 |
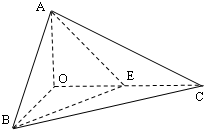 如图,已知三棱锥O-ABC的侧棱OA,OB,OC两两垂直,且OA=1,OB=OC=2,E是OC的中点.
如图,已知三棱锥O-ABC的侧棱OA,OB,OC两两垂直,且OA=1,OB=OC=2,E是OC的中点. 已知,如图四棱锥P-ABCD中,底面ABCD是平行四边形,PG⊥平面ABCD,垂足为G,G在线段AD上,且PG=4,
已知,如图四棱锥P-ABCD中,底面ABCD是平行四边形,PG⊥平面ABCD,垂足为G,G在线段AD上,且PG=4,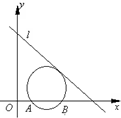 已知如图,直线l:x+y-5=0,圆C经过A(1,0)、B(3,0)两点,且与直线l相切,圆心C在第一象限.
已知如图,直线l:x+y-5=0,圆C经过A(1,0)、B(3,0)两点,且与直线l相切,圆心C在第一象限.