题目内容
17.已知复数z=x+(x-a)i,若对任意实数x∈(1,2),恒有|z|>|$\overline{z}$+i|,则实数a的取值范围为( )| A. | (-∞,$\frac{1}{2}$] | B. | (-∞,$\frac{1}{2}$) | C. | [$\frac{3}{2}$,+∞) | D. | ($\frac{3}{2}$,+∞) |
分析 求出复数的模,把|z|>|$\overline{z}$+i|,转化为a<x$-\frac{1}{2}$(1<x<2)恒成立,再求出x-$\frac{1}{2}$的范围得答案.
解答 解:∵z=x+(x-a)i,且|z|>|$\overline{z}$+i|恒成立,
∴$\sqrt{{x}^{2}+(x-a)^{2}}$>$\sqrt{{x}^{2}+(1+a-x)^{2}}$,
两边平方并整理得:a<x-$\frac{1}{2}$.
∵x∈(1,2),∴x-$\frac{1}{2}$∈($\frac{1}{2}$,$\frac{3}{2}$).
则a$≤\frac{1}{2}$.
∴实数a的取值范围为(-∞,$\frac{1}{2}$].
故选:A.
点评 本题考查复数模的求法,考查恒成立问题的求解方法,运用了分离变量法,是中档题.

练习册系列答案
相关题目
12.已知函数f(x)=$\left\{\begin{array}{l}{-\frac{3x+2}{x+1},x∈(-1,0]}\\{x,x∈(0,1]}\end{array}\right.$且g(x)=mx+m,若g(x)=f(x)在(-1,1]内有且仅有两个不同的根,则实数m的取值范围是( )
| A. | (-$\frac{9}{4}$,-2]∪(0,$\frac{1}{2}$] | B. | (-$\frac{11}{4}$,-2]∪(0,$\frac{1}{2}$] | C. | (-$\frac{9}{4}$,-2]∪(0,$\frac{2}{3}$] | D. | (-$\frac{11}{4}$,-2]∪(0,$\frac{2}{3}$] |
8.若集合A={x|-3<x<2},B={x|0<x<3},则A∩B=( )
| A. | {x|-3<x<0} | B. | {x|-3<x<3} | C. | {x|0<x<2} | D. | {x|0<x<3} |
2.在一个口袋中装有大小相同的5个白球和3个黑球,从中摸出3个球,至少摸到2个黑球的概率为( )
| A. | $\frac{9}{28}$ | B. | $\frac{3}{8}$ | C. | $\frac{3}{7}$ | D. | $\frac{2}{7}$ |
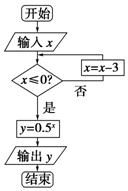 如图所示的程序框图,当输入x的值为3时,则其输出的结果是1.
如图所示的程序框图,当输入x的值为3时,则其输出的结果是1.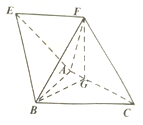 如图,在四棱锥A-EFCB中,四边形EFCB是梯形,EF∥BC且EF=$\frac{3}{4}$BC,△ABC是边长为2的正三角形,顶点F在AC上射影为点G,且FG=$\sqrt{3}$,CF=$\frac{{\sqrt{21}}}{2}$,BF=$\frac{5}{2}$.
如图,在四棱锥A-EFCB中,四边形EFCB是梯形,EF∥BC且EF=$\frac{3}{4}$BC,△ABC是边长为2的正三角形,顶点F在AC上射影为点G,且FG=$\sqrt{3}$,CF=$\frac{{\sqrt{21}}}{2}$,BF=$\frac{5}{2}$.