题目内容
14.通过随机询问110名性别不同的大学生是否爱好某项运动,得到如下的列联表:| 男 | 女 | 总计 | |
| 爱好 | 40 | 20 | 60 |
| 不爱好 | 20 | 30 | 50 |
| 总计 | 60 | 50 | 110 |
附表
| P(K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3,841 | 6.635 | 10.828 |
分析 根据条件中所给的观测值,同题目中节选的观测值表进行检验,得到观测值对应的结果,得到结论有99%以上的把握认为“爱好该项运动与性别有关”.
解答 解:由K2=$\frac{110×(40×30-20×20)^{2}}{60×50×60×50}$≈7.822>6.635,
∴有99%以上的把握认为爱好该项运动与性别有关.
点评 本题考查独立性检验的应用,考查对于观测值表的认识,这种题目一般运算量比较大,主要要考查运算能力,属于基础题.

练习册系列答案
相关题目
2.在一个口袋中装有大小相同的5个白球和3个黑球,从中摸出3个球,至少摸到2个黑球的概率为( )
| A. | $\frac{9}{28}$ | B. | $\frac{3}{8}$ | C. | $\frac{3}{7}$ | D. | $\frac{2}{7}$ |
3.某超市为了解顾客的购物量及结算时间等信息,安排一名员工随机收集了在该超市购物的100位顾客的相关数据,如表所示.
已知这100位顾客中的一次购物量超过8件的顾客占55%.
(1)确定x,y的值,并求顾客一次购物的结算时间X的分布列与数学期望;
(2)若某顾客到达收银台时前面恰有2位顾客需结算,且各顾客的结算相互独立,求该顾客结算前的等候时间不超过3 钟的概率.(注:将频率视为概率)
| 一次购物量 | 1至4件 | 5至8件 | 9至12件 | 13至16件 | 17件及以上 |
| 顾客数(人) | x | 30 | 25 | y | 10 |
| 结算时间(分钟/人) | 1 | 1.5 | 2 | 2.5 | 3 |
(1)确定x,y的值,并求顾客一次购物的结算时间X的分布列与数学期望;
(2)若某顾客到达收银台时前面恰有2位顾客需结算,且各顾客的结算相互独立,求该顾客结算前的等候时间不超过3 钟的概率.(注:将频率视为概率)
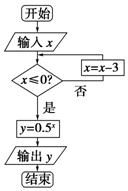 如图所示的程序框图,当输入x的值为3时,则其输出的结果是1.
如图所示的程序框图,当输入x的值为3时,则其输出的结果是1. 如图,已知正方形ABCD和矩形ACEF所在平面相互垂直,$AB=\sqrt{2},AF=1$,M在线段EF上.
如图,已知正方形ABCD和矩形ACEF所在平面相互垂直,$AB=\sqrt{2},AF=1$,M在线段EF上.