Question

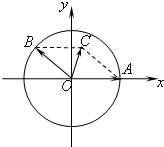如图，在xoy平面上，点A（1，0），点B在单位圆上，∠AOB=θ（0＜θ＜π）
（1）若点B（-

3

5

，

4

5

），求tan（

θ

2

+

π

4

）的值；
（2）若

OA

+

OB

=

OC

，四边形OACB的面积用S_θ表示，求S_θ+

OA

•

OC

的取值范围．

Answer 1

考点：平面向量数量积的运算,三角函数线

专题：平面向量及应用

分析：（1）利用任意角的三角函数定义可得sinθ，cosθ，再利用半角公式tan

θ

2

=

sinθ

1+cosθ

和两角和差的正切公式tan(

θ

2

+

π

4

)=

1+tan θ 2

1-tan θ 2

即可得出；
（2）利用向量的数量积运算法则、平行四边形的面积计算公式可得Sθ+

OA

•

OC

=sinθ+cosθ+1，再利用两角和的正弦公式即可得出．

解答： 解：（1）∵B(-

3

5

，

4

5

)，∠AOB=θ，
∴cosθ=-

3

5

，sinθ=

4

5

．
∴tan

θ

2

=

sinθ

1+cosθ

=

4 5

1- 3 5

=2．
∴tan(

θ

2

+

π

4

)=

1+tan θ 2

1-tan θ 2

=

1+2

1-2

=-3．
（2）S_θ=|OA||OB|sinθ=sinθ，
∵

OA

=（1，0），

OB

=（cosθ，sinθ），
∴

OC

=

OA

+

OB

=（1+cosθ，sinθ），
∴

OA

•

OC

=1+cosθ，
∴Sθ+

OA

•

OC

=sinθ+cosθ+1=

2

sin(θ+

π

4

)+1（0＜θ＜π），
∵

π

4

＜θ+

5π

4

＜

5π

4

，
∴-

2

2

＜sin(θ+

π

4

)≤1，
∴0＜Sθ+

OA

•

OC

≤

2

+1．

点评：本题综合考查了任意角的三角函数定义、半角公式、两角和差的正切公式、向量的数量积运算法则、平行四边形的面积计算公式、两角和的正弦公式等基础知识与基本技能方法，属于中档题．