题目内容
已知命题p:直线y=x+t与抛物线y2=4x有两个交点;命题q:关于x的方程x2-tx+4=0有实根.若p∨q为真命题,p∧q为假命题,求实数t的取值范围.
考点:直线与圆锥曲线的关系,复合命题的真假
专题:圆锥曲线的定义、性质与方程,简易逻辑
分析:由于直线y=x+t与抛物线y2=4x有两个交点
有两个解,解出参数的范围,化简p条件,再由关于x的方程x2-tx+4=0有实根得出△=t2-16≥0,解出q条件,然后再由复合命题的真假得出实数t的取值范围即可
|
解答:
解:命题p:直线y=x+t与抛物线y2=4x有两个交点,则
有两个解,即y2=4(y-t)有两个根,故有△=16-16t>0,解得t<1,
命题q:关于x的方程x2-tx+4=0有实根,则△=t2-16≥0,解得t≥4或t≤-4
因为p∨q为真命题,p∧q为假命题,所以p与q一真一假
若p真q假,则
,解得-4<t<1
若p假q真,则
,解得t≥4
综上,实数t的取值范围为-4<t<1或t≥4
|
命题q:关于x的方程x2-tx+4=0有实根,则△=t2-16≥0,解得t≥4或t≤-4
因为p∨q为真命题,p∧q为假命题,所以p与q一真一假
若p真q假,则
|
若p假q真,则
|
综上,实数t的取值范围为-4<t<1或t≥4
点评:本题考查了直线与抛物线相交的位置关系的转化,复合命题的真假判断,知识性强,综合性强,解答时要认真审题,正确转化方能顺利解答

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
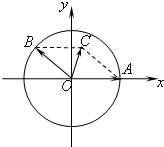 如图,在xoy平面上,点A(1,0),点B在单位圆上,∠AOB=θ(0<θ<π)
如图,在xoy平面上,点A(1,0),点B在单位圆上,∠AOB=θ(0<θ<π)