题目内容
数列2，5，11，20，x，47，…中的x等于（ ）
| A、28 | B、27 | C、33 | D、32 |
考点：数列的概念及简单表示法
专题：等差数列与等比数列
分析：本题可先用加、减、乘、除等对数列对已知几项进行拆分研究，发现规律后，再运用规律解决问题．
解答：
解：∵数列的前几项为2，5，11，20，x，47，
其中5-2=3，
11-5=6
20-11=9，
猜想：x-20=12，
47-x=15，
而x=32时，正好满足上述要求．
故答案为：D
其中5-2=3，
11-5=6
20-11=9，
猜想：x-20=12，
47-x=15，
而x=32时，正好满足上述要求．
故答案为：D
点评：本题考查的是数列知识，实质是要发现这列数的规律，要注意本题的规律不唯一．
练习册系列答案
阅读快车系列答案
相关题目
函数y=lnsin（-2x+
）的单调递减区间为 （ ）
| π |
| 3 |
A、（kπ+
| ||||
B、（kπ+
| ||||
C、（kπ+
| ||||
D、[kπ-
|
已知等差数列{an}的前n项和为Sn，S10=0，且Sn≥-5对一切n∈N*恒成立，则此等差数列{an}公差d的取值范围是（ ）
A、（-∞，
| ||
B、[0，
| ||
C、[-
| ||
D、[0，
|
设全集U是实数集R，集合M={x|x2≥2x}，N={x|log2（x-1）≤0}，则M∩N=（ ）
| A、{1，2} |
| B、{ 2 } |
| C、{1} |
| D、[1，2] |
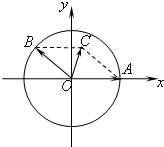如图，在xoy平面上，点A（1，0），点B在单位圆上，∠AOB=θ（0＜θ＜π）