题目内容

20．已知函数f（x）=（x-b）lnx+x2在区间[1，e]上单调递增，则实数b的取值范围是（　　）
A．（-∞，-3]B．（-∞，2e]C．（-∞，3]D．（-∞，2e2+2e]

分析 令f′（x）≥0在[1，e]上恒成立，对b进行讨论得出b的范围．

解答 解：f′（x）=lnx+$\frac{x-b}{x}$+2x=lnx-$\frac{b}{x}$+1+2x，
∵f（x）在[1，e]上单调递增，∴f′（x）≥0在[1，e]上恒成立，
若b≤0，显然f′（x）＞0恒成立，符合题意，
若b＞0，则f′′（x）=$\frac{1}{x}$+$\frac{b}{{x}^{2}}$+2＞0，
∴f′（x）在[1，e]上是增函数，
∴f′（x）≥f′（1）≥0，即-b+1+2≥0，解得0＜b≤3，
综上，b的范围是（-∞，3]．
故选：C．

点评 本题考查了函数的单调性与导数的关系，函数的最值计算，属于中档题．

练习册系列答案
相关题目
3．在等差数列{an}中，a3，a15是方程x2-6x-10=0的根，则S17的值是（　　）
A．41B．51C．61D．68
11．已知x，y∈R，m+n=7，f（x）=|x-1|-|x+1|．
（1）解不等式f（x）≥（m+n）x；
（2）设max{a，b}=$\left\{\begin{array}{l}{a（a≥b）}\\{b（a＜b）}\end{array}\right.$，求F=max{|x2-4y+m|，|y2-2x+n|}的最小值．
8．已知$\overrightarrow a，\overrightarrow b$是单位向量，$\overrightarrow a，\overrightarrow b$的夹角为90°，若向量$\overrightarrow c满足$|$\overrightarrow c-\overrightarrow a-\overrightarrow b|=2$，则$\overrightarrow{|c}$|的最大值为（　　）
A．$2-\sqrt{2}$B．$\sqrt{2}$C．2D．$2+\sqrt{2}$
15．设正实数x，y，则|x-y|+$\frac{1}{x}$+y2的最小值为（　　）
A．$\frac{7}{4}$B．$\frac{3\root{3}{2}}{2}$C．2D．$\root{3}{2}$
5．已知函数f（x）=ax-lnx+x2．
（Ⅰ）若a=-1，求函数f（x）的极值；
（Ⅱ）若a=1，?x1∈（1，2），?x2∈（1，2），使得f（x1）-x12=mx2-$\frac{1}{3}m{x_2}$3（m≠0），求实数m的取值范围．
12．已知函数f（x）=alnx+x2-（a+2）x恰有两个零点，则实数a的取值范围是（　　）
A．（-1，+∞）B．（-2，0）C．（-1，0）D．（-2，-1）
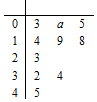9．已知函数$f（x）={x^2}+\sqrt{2}（m-1）x+\frac{m}{4}$，现有一组数据（数据量较大），从中随机抽取10个，绘制所得的茎叶图如图所示，且茎叶图中的数据的平均数为2．（茎叶图中的数据均为小数，其中茎为整数部分，叶为小数部分）
（Ⅰ）现从茎叶图的数据中任取4个数据分别替换m的值，
求至少有2个数据使得函数f（x）没有零点的概率；
（Ⅱ）以频率估计概率，若从该组数据中随机抽取4个数据分别替换m的值，记使得函数f（x）没有零点的个数为ξ，求ξ的分布列及数学期望．
10．已知实数x，y满足$\left\{\begin{array}{l}{2x-y-2≥0}\\{x+y-1≤0}\\{y+1≥0}\end{array}\right.$，z=mx+y的最大值为3，则实数m的值是（　　）
A．-2B．3C．8D．2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网