题目内容
15.设正实数x,y,则|x-y|+$\frac{1}{x}$+y2的最小值为( )| A. | $\frac{7}{4}$ | B. | $\frac{3\root{3}{2}}{2}$ | C. | 2 | D. | $\root{3}{2}$ |
分析 利用绝对值不等式化简即可得出结论.
解答 解:∵x>0,y>0,
∴|x-y|+$\frac{1}{x}$+y2=|x-y|+|$\frac{1}{x}$|+|y2|≥|x-y+$\frac{1}{x}$+y2|=|(y-$\frac{1}{2}$)2+(x+$\frac{1}{x}$)-$\frac{1}{4}$|≥|2-$\frac{1}{4}$|=$\frac{7}{4}$.
当且仅当y=$\frac{1}{2}$,x=$\frac{1}{x}$即x=1,y=$\frac{1}{2}$时取等号.
故选A.
点评 本题考查了绝对值不等式的性质,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.已知角α的终边与单位圆x2+y2=1的交点为$P\;(x\;,\frac{{\sqrt{3}}}{2})$,则cos2α=( )
| A. | $\frac{1}{2}$ | B. | $-\frac{1}{2}$ | C. | $-\frac{{\sqrt{3}}}{2}$ | D. | 1 |
6.为调查高中生的数学成绩与学生自主学习时间之间的相关关系,某重点高中数学教师对新入学的45名学生进行了跟踪调查,其中每周自主做数学题的时间不少于15小时的有19人,余下的人中,在高三模拟考试中数学平均成绩不足120分的占$\frac{8}{13}$,统计成绩后,得到如下的2×2列联表:
(Ⅰ)请完成上面的2×2列联表,并判断能否在犯错误的概率不超过0.01的前提下认为“高中生的数学成绩与学生自主学习时间有关”;
(Ⅱ)( i) 按照分层抽样的方法,在上述样本中,从分数大于等于120分和分数不足120分的两组学生中抽取9名学生,设抽到的不足120分且周做题时间不足15小时的人数是X,求X的分布列(概率用组合数算式表示);
( ii) 若将频率视为概率,从全校大于等于120分的学生中随机抽取20人,求这些人中周做题时间不少于15小时的人数的期望和方差.
附:${K^2}=\frac{{n{{(ad-bc)}^2}}}{{({a+b})({c+d})({a+c})({b+d})}}$
| 分数大于等于120分 | 分数不足120分 | 合 计 | |
| 周做题时间不少于15小时 | 15 | 4 | 19 |
| 周做题时间不足15小时 | 10 | 16 | 26 |
| 合 计 | 25 | 20 | 45 |
(Ⅱ)( i) 按照分层抽样的方法,在上述样本中,从分数大于等于120分和分数不足120分的两组学生中抽取9名学生,设抽到的不足120分且周做题时间不足15小时的人数是X,求X的分布列(概率用组合数算式表示);
( ii) 若将频率视为概率,从全校大于等于120分的学生中随机抽取20人,求这些人中周做题时间不少于15小时的人数的期望和方差.
附:${K^2}=\frac{{n{{(ad-bc)}^2}}}{{({a+b})({c+d})({a+c})({b+d})}}$
| P(K2≥k0) | 0.050 | 0.010 | 0.001 |
| k0 | 3.841 | 6.635 | 10.828 |
10.已知函数f(x)=$\left\{{\begin{array}{l}{lnx,x>0}\\{\frac{m}{x},x<0}\end{array}}$,若f(x)-f(-x)=0有四个不同的根,则m的取值范围是( )
| A. | (0,2e) | B. | (0,e) | C. | (0,1) | D. | (0,$\frac{1}{e}$) |
20.已知函数f(x)=(x-b)lnx+x2在区间[1,e]上单调递增,则实数b的取值范围是( )
| A. | (-∞,-3] | B. | (-∞,2e] | C. | (-∞,3] | D. | (-∞,2e2+2e] |
7.若从集合{1,2,3,5}中随机地选出三个元素,则满足其中两个元素的和等于第三个元素的概率为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{1}{3}$ |
4.已知集合A={-1,0,1},B={y|y=2x-2,x∈A},则A∩B=( )
| A. | {0,1} | B. | {-1,1} | C. | {-1,0} | D. | {-1,0,1} |
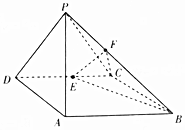 如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,底面ABCD是平行四边形,∠ABC=45°,AD=AP=2,AB=DP=2$\sqrt{2}$,E为CD的中点,点F在线段PB上.
如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,底面ABCD是平行四边形,∠ABC=45°,AD=AP=2,AB=DP=2$\sqrt{2}$,E为CD的中点,点F在线段PB上.