题目内容
已知A三角形ABC的内角,则“sinA=
”是“cosA=
”的( )
| ||
| 2 |
| ||
| 2 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
考点:必要条件、充分条件与充要条件的判断
专题:简易逻辑
分析:根据三角函数的关系,结合充分条件和必要条件的定义即可得到结论.
解答:
解:在△ABC中,若sinA=
,则A=
或
,当A=
时,cosA=-
,即充分性不成立,
若cosA=
,则A=
,此时sinA=
,∴必要性成立,
∴“sinA=
”是“cosA=
”的必要不充分条件,
故选:B
| ||
| 2 |
| π |
| 4 |
| 3π |
| 4 |
| 3π |
| 4 |
| ||
| 2 |
若cosA=
| ||
| 2 |
| π |
| 4 |
| ||
| 2 |
∴“sinA=
| ||
| 2 |
| ||
| 2 |
故选:B
点评:本题主要考查充分条件和必要条件的判断,利用三角函数的图象和性质是解决本题的关键.

练习册系列答案
相关题目
在平行四边形ABCD中,
=
,
=
,
=3
,M为BC的中点,则
=( )
| AB |
| a |
| AD |
| b |
| AN |
| NC |
| MN |
A、-
| ||||||||
B、-
| ||||||||
C、
| ||||||||
D、-
|
设全集U={3,4,5,6},集合A={3,5,6},B={4,5,6},则∁UA∩B=( )
| A、{4,7} | B、{3,6} |
| C、{4} | D、{7} |
若曲线y=x2+ax+b在点(1,b)处的切线方程是x-y+1=0,则( )
| A、a=1,b=2 |
| B、a=-1,b=2 |
| C、a=1,b=-2 |
| D、a=-1,b=-2 |
设复数z满足z•(i-1)=2i(其中i为虚数单位),则z等于( )
| A、1-i | B、1+i |
| C、-1+i | D、-1-i |
下列命题中的真命题是( )
| A、?x∈R,x2>0 | ||
B、?x∈R,x+
| ||
| C、?x0∈R,sinx0+cosx0=2 | ||
D、?x0∈R,ln x0>(
|
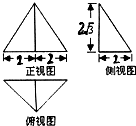 一个几何体的三视图如图所示,其中正视图是正三角形,则该几何体的三个侧棱与地面所成的角的集合为
一个几何体的三视图如图所示,其中正视图是正三角形,则该几何体的三个侧棱与地面所成的角的集合为 2013年4月20日8点02分四川省雅安市芦山县(北纬30.3度,东经103.0度)
2013年4月20日8点02分四川省雅安市芦山县(北纬30.3度,东经103.0度)