题目内容
△ABC的内角A、B、C所对的边分别为a、b、c,若△ABC的面积S=
[a2-(b-c)2],则
等于( )
| 1 |
| 2 |
| 1-cosA |
| sinA |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:余弦定理
专题:解三角形
分析:根据余弦定理和三角形的面积公式建立条件关系即可得到结论.
解答:
解:由三角形的面积公式可得
bcsinA=
[a2-(b-c)2],
即bcsinA=a2-b2-c2+2bc,
则b2+c2-a2=2bc-bcsinA,
由余弦定理得cosA=
=
=1-
sinA,
即1-cosA=
sinA,
∴
=
,
故选:A.
| 1 |
| 2 |
| 1 |
| 2 |
即bcsinA=a2-b2-c2+2bc,
则b2+c2-a2=2bc-bcsinA,
由余弦定理得cosA=
| b2+c2-a2 |
| 2bc |
| 2bc-bcsinA |
| 2bc |
| 1 |
| 2 |
即1-cosA=
| 1 |
| 2 |
∴
| 1-cosA |
| sinA |
| 1 |
| 2 |
故选:A.
点评:本题主要考查解三角形的应用,利用余弦定理和三角形的面积公式是解决本题的关键.

练习册系列答案
相关题目
i+i2+i3+…+i2014=( )
| A、1+i | B、-1-i |
| C、1-i | D、-1+i |
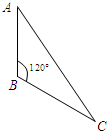 在△ABC中,AB=3,BC=4,∠ABC=120°,若把△ABC绕直线AB旋转一周,则所形成的几何体的体积是( )
在△ABC中,AB=3,BC=4,∠ABC=120°,若把△ABC绕直线AB旋转一周,则所形成的几何体的体积是( )| A、11π | B、12π |
| C、13π | D、14π |
设x,y满足约束条件
,若目标函数z=ax+by(a,b>0)的最大值是12,则a2+b2的最小值是( )
|
A、
| ||
B、
| ||
C、
| ||
D、
|
一个几何体的三视图如图所示,则该几何体的体积为( )


| A、1 | ||
B、
| ||
C、
| ||
D、
|
已知
=(1,2,-1),则向量
的模的大小为( )
| a |
| a |
| A、4 | ||
| B、6 | ||
C、
| ||
D、
|
已知命题P:复数z=
在复平面内所对应的点位于第四象限;命题q:?x>0,x=cosx,则下列命题中为真命题的是( )
| 1+i |
| i |
| A、(¬p)∧(¬q) |
| B、(¬p)∧q |
| C、p∧(¬q) |
| D、p∧q |