Question

设x，y满足约束条件

3x-y-6≤0 x-y+2≥0 x，y≥0

，若目标函数z=ax+by（a，b＞0）的最大值是12，则a²+b²的最小值是（　　）

• A、

  6

  13

• B、

  36

  5

• C、

  6

  5

• D、

  36

  13

Answer 1

考点：简单线性规划

专题：不等式的解法及应用

分析：作出不等式对应的平面区域，利用目标函数z=ax+by（a＞0，b＞0）的最大值是12，确定a，b之间的关系，利用两点间的距离公式进行求解即可．．

解答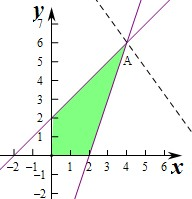： 解：作出不等式对应的平面区域如图：
由z=ax+by（a＞0，b＞0），
得y-

a

b

x+

z

b

，
平移直线y-

a

b

x+

z

b

，由图象可知当直线y-

a

b

x+

z

b

经过点A时，直线y-

a

b

x+

z

b

的截距最大，此时确定最大值12，
由

3x-y-6=0 x-y+2=0

，
解得

x=4 y=6

，即A（4，6），
代入目标函数得4a+6b=12，
即2a+3b=6，对应曲线为直线，
设m=a²+b²，
则m的几何意义是直线2a+3b=6上的点到原点的距离的平方，
原点到直线2a+3b=6的距离d=

|6|

22+32

=

6

13

，
∴a²+b²的最小值m=d²=

36

13

，
故选：D．

点评：本题主要考查线性规划的应用，利用目标函数的几何意义，确定a，b的关系是解决本题的关键．