题目内容
求下列函数的定义域:
(1)y=
+
;
(2)y=
;
(3)y=
-
-
.
(1)y=
| x+2 |
| 1 |
| x2-x-6 |
(2)y=
| (x+1)0 | ||
|
(3)y=
| 5-x |
| x-5 |
| 1 |
| x2-9 |
考点:函数的定义域及其求法
专题:函数的性质及应用
分析:应用直接由根式内部的代数式大于等于0,分母不为0,联立取交集即可.
解答:
解:(1)要使函数有意义,则
,解得x>-2且x≠3,所以原函数的定义域为(-2,3)∪(3,+∞);
(2)要使函数有意义,则
,解得x<0且x≠-1,所以原函数的定义域为(-∞,-1)∪(-1,0);
(3)要使函数有意义,首先应满足
,解得x=5,而当x=5时也满足x2-9≠0,所以原函数的定义域为{x|x=5}.
|
(2)要使函数有意义,则
|
(3)要使函数有意义,首先应满足
|
点评:本题考查了函数的定义域及其求法,函数的定义域就是使函数解析式有意义的自变量x的取值范围,是基础题

练习册系列答案
相关题目
由a1=1,d=3确定的等差数列{an},当an=268时,序号n等于( )
| A、80 | B、100 | C、90 | D、88 |
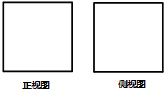 右图是边长相等的两个正方形.则下列三个命题中正确的个数( )
右图是边长相等的两个正方形.则下列三个命题中正确的个数( )